< 인공신경망 >
인공신경망(ANN)
├── 단층신경망(SLP) (은닉층 없음)
├── 다층신경망(MLP) (은닉층 1개 이상)
│ ├── 심층신경망(DNN) (은닉층 3개 이상)
인공신경망(ANN)은 다층신경망(MLP)과 심층신경망(DNN)을 모두 포함하는 상위 개념
ANN ⊃ MLP ⊃ DNN
ANN(Artificial Neural Network)
인공신경망(Artificial Neural Network, ANN)은 인간의 뇌 구조를 모방한 기계 학습 모델로, 주로 패턴 인식, 분류, 예측 등의 문제 해결에 사용된다.

| 생물학적 뉴런 | 인공 뉴런 |
| 수상돌기(Dendrite) → 다른 뉴런으로부터 신호(입력)를 받음 | 입력(Inputs, x₀, x₁, ...) → 데이터를 입력받음 |
| 세포체(Cell Body) → 신호를 처리 | 가중치(Weight, w₀, w₁, ...) → 각 입력값에 중요도를 부여 |
| 축삭(Axon Terminal) → 다른 뉴런으로 신호를 전달 | 활성 함수(Activation Function) → 최종 출력값을 결정 |
- ∑ → 각 입력값에 가중치를 곱한 후 모두 더하는 과정
- 활성함수 : 시그모이드(Sigmoid), 하이퍼볼릭 탄젠트(tanh), 렐루(ReLU), 소프트맥스(Softmax) 등..

단층신경망(SLP, Single Layer Perceptron)
단층신경망(SLP, Single Layer Perceptron)은 가장 기본적인 인공 신경망(Artificial Neural Network, ANN)의 한 종류. 입력층(Input Layer)과 출력층(Output Layer)으로 구성되며, 은닉층(Hidden Layer)이 없는 형태.
이 모델은 선형 분류 문제(linear classification)를 해결할 수 있으며, 대표적으로 논리 AND, OR 같은 간단한 문제를 해결하는 데 적합하다. 하지만 XOR 문제처럼 비선형적으로 구분해야 하는 문제는 해결할 수 없다.
- Single Layer Perceptron (SLP)
import numpy as np
# 시그모이드 활성화 함수
# 입력값 z에 대해 시그모이드 활성화 함수를 적용하는 함수 정의
def sigmoid(z):
return 1 / (1 + np.exp(-z))
# SLP 순전파 구현 (하드 코딩된 가중치와 편향)
# 입력데이터 X, 가중치 W, 편향 b를 받아서 순방향 학습하도록 함수 정의 (순전파)
# np.dot(W, X)는 가중치와 입력데이터 간의 행렬 곱을 계산하고 이 결과에 편향 b를 더한 후, 시그모이드 함수를 통해 최종 출력하여 계산결과를 도출한다.
def forward_slp(X, W, b):
Z = np.dot(W, X) + b # 선형 변환
A = sigmoid(Z) # 시그모이드 활성화 함수 적용
return A
# 이렇게 함으로써 입력 데이터가 뉴런을 통과한 후의 최종 출력값을 얻을 수 있다.
# 입력 데이터 예시 (특징 3개)
# 3개의 특성을 가진 입력 데이터 X에 배열 형태로 대입
X = np.array([[1], [2], [3]]) # 입력 데이터
# 하드코딩된 가중치와 편향 (설정)
# 3개의 입력 특성에 각각 0.2, 0.4, 0.6 으로 가중치를 할당하고 편향으로 0.5를 정의한다.
W = np.array([[0.2, 0.4, 0.6]]) # 1x3 크기 (하나의 노드)
b = np.array([[0.5]]) # 편향
# 가중치는 각 입력값(X)과 곱해지고, 편향은 결과값에 더해져서 모델이 특정 방향으로 조정될 수 있도록 한다.
# SLP 순전파 수행
# forward_slp() 함수를 기반으로 정의한 입력데이터 X, 가중치 W, 편향 b 사용하여 순방향 학습 결과를 도출한다.
output_slp = forward_slp(X, W, b)
# forward_slp함수 결과를 출력한다.
print("Single Layer Perceptron 출력:", output_slp)
# 현재 코드는 가중치(W)와 편향(b)이 고정되어 있어서 학습이 불가능.
# 즉, 입력값이 주어지면 항상 같은 결과를 내는 하드코딩된 SLP.
# 실제 머신러닝 모델은 가중치와 편향을 학습을 통해 조정해야 함.
Single Layer Perceptron (SLP): 입력 데이터 X = [1, 2, 3] 에 대해 하드코딩된 가중치 W = [0.2, 0.4, 0.6] 와 편향 b = 0.5 을 적용하여 수행한다. 시그모이드 활성화 함수로 출력값을 계산한다.
※
1. 비선형 변환
SLP에서 sigmoid 함수와 같은 비선형 변환을 사용하는 이유는, 입력 신호를 일정한 범위(0과 1 사이)로 변환하여 출력값을 조정하는 것이다. 이를 통해, SLP는 출력값이 선형적인 형태를 넘어서서 비선형적인 특성을 가지게 된다. 하지만, 이 비선형 변환은 단일 계층 구조에서는 복잡한 비선형 분류 문제를 해결하는 데는 한계가 있다.
2. 비선형 구분 문제
비선형 구분 문제는 데이터가 직선이나 평면 같은 선형적인 형태로 구분되지 않고, 더 복잡한 형태로 구분이 필요할 때를 말한다. 예를 들어, XOR 문제처럼 데이터가 두 그룹으로 나뉘는데, 그 경계가 직선으로 나눠지지 않으면 비선형 구분이 필요하다.
SLP는 비선형 변환을 할 수 있지만, 하나의 선형 결정 경계만 만들 수 있기 때문에 비선형 구분 문제는 해결할 수 없다. 즉, SLP는 입력과 출력 사이에 비선형 변환을 적용할 수는 있지만, 비선형적으로 구분해야 하는 문제는 해결하지 못한다. 이 문제는 다층 퍼셉트론(MLP, Multi-Layer Perceptron) 같은 더 복잡한 구조에서 해결할 수 있다.
다층신경망(MLP, Multi- Layer Perceptron)
다층신경망(Multi-Layer Perceptron, MLP)은 단층신경망(SLP)의 확장된 형태. SLP는 입력층과 출력층만 가지고 있지만, MLP는 하나 이상의 은닉층(hidden layers)을 추가하여 복잡한 문제를 해결할 수 있다.
MLP의 구성 요소:
- 입력층 (Input Layer): 입력 데이터를 받아들이는 부분.
- 은닉층 (Hidden Layer): 여러 개의 은닉층을 가질 수 있으며, 이 층에서 데이터를 비선형적으로 변환하고 특징을 추출한다. 각 층은 뉴런으로 구성되며, 각 뉴런은 가중치와 편향을 통해 신호를 변환한다.
- 출력층 (Output Layer): 최종 결과를 출력하는 부분.
※ 입력층과 출력층에도 각각 뉴런들이 존재하고, 은닉층에서 뉴런들이 복잡한 변환을 수행하면서 데이터를 처리한다는 점에서 세 가지 층 모두 뉴런으로 구성된다.
MLP의 특징:
- 비선형 문제 해결 가능: MLP는 여러 개의 은닉층을 통해 비선형적으로 구분되는 문제도 해결할 수 있다. 이 때문에 XOR 문제 같은 복잡한 문제도 해결할 수 있다.
- 비선형 활성화 함수: MLP에서 은닉층에 사용되는 활성화 함수(예: sigmoid, ReLU 등)는 비선형 함수로, 네트워크가 비선형적인 관계를 학습할 수 있도록 도와준다.
- 학습 방식: MLP는 역전파(backpropagation) 알고리즘을 사용해 가중치와 편향을 최적화하며 학습을 진행한다.
SLP와 MLP의 차이점:
- SLP는 하나의 선형 분류기로, 하나의 결정 경계를 만들 수 있다. 하지만 MLP는 여러 은닉층을 통해 비선형적으로 데이터를 구분할 수 있기 때문에 훨씬 더 복잡한 문제를 해결할 수 있다.
따라서 MLP는 다층 신경망으로 더 많은 층을 통해 더 복잡하고 비선형적인 패턴을 학습할 수 있다는 점이 SLP와 가장 큰 차이이다.
- Multi-Layer Perceptron (MLP)
# ReLU 활성화 함수
# ReLU(Rectified Linear Unit)는 z가 0보다 크면 그대로 반환, 0보다 작으면 0으로 변환하는 함수
# 음수를 0으로 변환하면서 비선형성을 추가하고, 기울기 소실 문제를 완화
def relu(z):
return np.maximum(0, z)
# 소프트맥스 함수
# 소프트맥스(Softmax)는 다중 클래스 분류에서 확률 값을 출력할 때 사용
# 각 요소를 0~1 사이의 값으로 변환하고, 모든 요소의 합이 1이 되도록 정규화
# np.exp(z - np.max(z)) 부분은 오버플로우 방지(수치적 안정성)를 위한 처리.
def softmax(z):
exp_z = np.exp(z - np.max(z)) # 안정성을 위한 처리
return exp_z / np.sum(exp_z, axis=0)
# MLP 순전파 구현 (하드 코딩된 가중치와 편향)
# 입력 X와 하드코딩된 가중치 및 편향(parameters)을 이용해서 출력을 계산
def forward_mlp(X, parameters):
# 첫 번째 은닉층
W1 = parameters['W1'] # 은닉층의 가중치 (4개의 뉴런 X 입력 특징 3개)
b1 = parameters['b1'] # 은닉층의 편향 (4개의 뉴런)
Z1 = np.dot(W1, X) + b1 # 선형 변환
A1 = relu(Z1) # 비선형 변환(ReLU 적용)
# 출력층
W2 = parameters['W2'] # 출력층의 가중치 (2개의 뉴런 × 은닉층 뉴런 4개)
b2 = parameters['b2'] # 출력층의 편향 (2개의 뉴런)
Z2 = np.dot(W2, A1) + b2 # 선형 변환
A2 = softmax(Z2) # 비선형 변환(소프트맥스 적용)
return A2
# 전체 구조 : 입력층 (X) → (선형 변환) → 은닉층 (Z1) → (ReLU 활성화) → A1 → (선형 변환) → 출력층 (Z2) → (Softmax 활성화) → A2 (출력)
# 입력 데이터 예시 (특징 3개)
X = np.array([[1], [2], [3]]) # 입력 데이터
# 하드코딩된 가중치와 편향
parameters = {
'W1': np.array([[0.1, 0.2, 0.3], [0.4, 0.5, 0.6], [0.7, 0.8, 0.9], [1.0, 1.1, 1.2]]), # 은닉층 가중치 (4x3)
'b1': np.array([[0.1], [0.2], [0.3], [0.4]]), # 은닉층 편향 (4x1)
'W2': np.array([[0.1, 0.2, 0.3, 0.4], [0.5, 0.6, 0.7, 0.8]]), # 출력층 가중치 (2x4)
'b2': np.array([[0.1], [0.2]]) # 출력층 편향 (2x1)
}
# MLP 순전파
output_mlp = forward_mlp(X, parameters)
print("Multi-Layer Perceptron 출력:", output_mlp)위 코드는 학습을 포함하지 않고, 하드코딩된 가중치와 편향을 사용하여 SLP와 MLP의 순전파(Forward Propagation)만을 보여준다.
첫 번째 은닉층 가중치 W1 는 4개의 뉴런이므로 4x3 크기, 편향 b1 는 4x1 크기이다. 출력층 가중치 W2 는 2개의 출력 뉴런이므로 2x4 크기, 편향 b2 는 2x1 크기이다.
은닉층에서 ReLU를 사용해 비선형성을 추가함. 출력층에서 Softmax를 사용해 확률 값을 얻음.
이전의 SLP보다 더 복잡한 패턴을 학습할 수 있음.
- SLP: 이진 분류 문제에서 단순한 예측 결과를 출력.
- MLP: 은닉층을 포함하여 더 복잡한 다중 클래스 분류 문제를 해결.
인공신경망의 이론적 개념
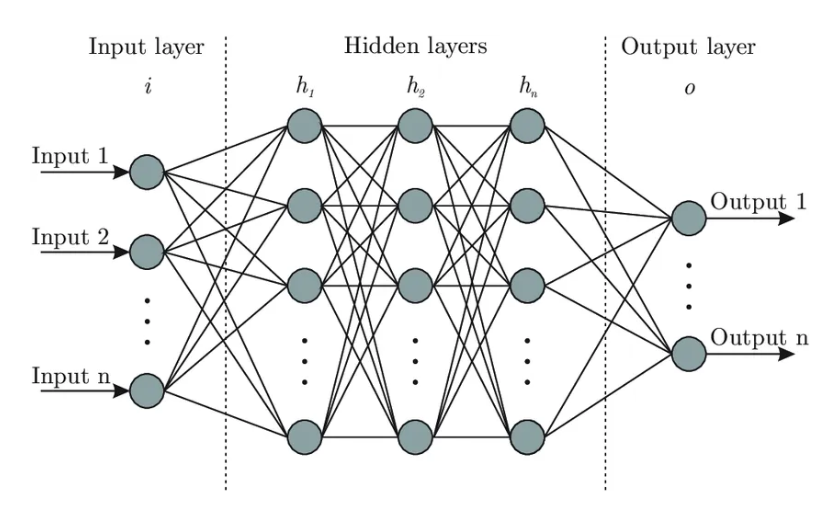
인공신경망은 여러 개의 뉴런(노드)이 레이어(층)로 배열된 구조로, 입력과 출력을 연결한다. 각 뉴런은 활성화 함수(activation function)를 통해 입력 신호를 처리하며, 가중치(weight)와 편향(bias)을 포함하여 학습이 진행된다.
주요 구성 요소:
- 입력층(Input Layer): 데이터가 처음 들어오는 층.
- 은닉층(Hidden Layer): 입력층과 출력층 사이에 위치한 층으로, 이 층에서 중요한 특징 추출이 이루어진다.
- 출력층(Output Layer): 최종 예측 결과가 나오는 층.
- 가중치(Weights): 각 연결에서 신호의 중요도를 나타낸다.
- 편향(Bias): 뉴런 활성화에 영향을 미치는 추가적인 요소.
* 회귀 : 출력 뉴런 1개, 선형 활성화 함수
* 이진분류 : 출력 뉴런 1개, 시그모이드 함수
* 다중 클래스 분류 : 출력뉴런 여러 개, 소프트맥스 함수
역전파의 기본 개념 (과정 순서)
- 순전파(Forward Propagation)
- 입력을 넣어서 출력을 계산
- 예측값(ŷ, y-hat)과 실제값(y)의 차이(오차)를 확인
- 오차 계산
- 손실 함수(Loss Function)로 예측값과 실제값의 차이를 측정
- 예: MSE(평균제곱오차, Mean Squared Error), 교차 엔트로피(Cross-Entropy)
- 오차를 줄이기 위한 가중치 업데이트
- 오차가 얼마나 가중치(W)에 영향을 받았는지(미분, Gradient) 계산
- 미분을 이용해 가중치를 조금씩 수정
- 이 과정을 역전파(Backpropagation)라고 한다.
- 반복하면서 학습 진행
- 여러 번 반복하면서 오차가 점점 줄어들도록 학습
→ 신경망을 학습시키는 과정에서, 출력과 실제 값 사이의 오차를 기반으로 가중치와 편향을 업데이트하는 과정이다. 이를 위해 경사 하강법(기울기 하강법, Gradient Descent)이 사용된다.
- 간단한 신경망에서 오차 역전파를 수행하는 코드 예시
import numpy as np
# 활성화 함수 (sigmoid) 및 도함수
# 시그모이드(Sigmoid) 함수는 값을 0~1 사이로 변환해서 확률처럼 사용할 수 있음.
# 도함수(sigmoid_derivative)는 역전파에서 기울기(Gradient)를 계산할 때 필요.
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def sigmoid_derivative(x):
return sigmoid(x) * (1 - sigmoid(x))
# 손실 함수 (Mean Squared Error)
# 평균 제곱 오차(MSE)를 손실 함수로 사용해서 예측값과 실제값의 차이를 계산.
# 신경망이 학습할 때, 손실을 줄이는 방향으로 가중치를 업데이트
def loss(y_true, y_pred):
return 0.5 * np.mean((y_true - y_pred) ** 2)
# 데이터 (입력과 실제 출력)
# X는 2개의 입력을 가지는 4개의 데이터셋.
# y는 XOR 연산 결과.
X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]]) # 입력 (XOR 문제)
y = np.array([[0], [1], [1], [0]]) # 실제 출력
# 가중치 및 편향 초기화 (무작위)
# W1 → 입력층(2개)에서 은닉층(2개)으로 가는 가중치
# b1 → 은닉층(2개) 편향
# W2 → 은닉층(2개)에서 출력층(1개)으로 가는 가중치
# b2 → 출력층(1개) 편향
# 무작위 초기화(random)를 사용해서 신경망이 다양한 방향으로 학습할 수 있도록 함.
W1 = np.random.randn(2, 2) # 입력층 -> 은닉층 가중치
b1 = np.random.randn(1, 2) # 은닉층 편향
W2 = np.random.randn(2, 1) # 은닉층 -> 출력층 가중치
b2 = np.random.randn(1, 1) # 출력층 편향
# 학습률 설정
# 학습률(learning rate)이란?
#"가중치를 얼마나 빠르게 업데이트할지 결정하는 값".
# 쉽게 말하면, 학습 속도를 조절하는 버튼.
learning_rate = 0.1
# 순전파 및 역전파 실행
for epoch in range(10000): # 10,000번 반복 학습
# 순전파 (Forward Propagation)
z1 = np.dot(X, W1) + b1
a1 = sigmoid(z1)
z2 = np.dot(a1, W2) + b2
a2 = sigmoid(z2) # 예측 출력
# 손실 계산
loss_value = loss(y, a2)
# 역전파 (Backpropagation)
# 출력층 오차
dL_da2 = a2 - y # 손실의 출력층에 대한 기울기
dL_dz2 = dL_da2 * sigmoid_derivative(z2)
# 은닉층 -> 출력층 가중치 및 편향 업데이트
dL_dW2 = np.dot(a1.T, dL_dz2)
dL_db2 = np.sum(dL_dz2, axis=0, keepdims=True)
# 은닉층 오차
dL_da1 = np.dot(dL_dz2, W2.T)
dL_dz1 = dL_da1 * sigmoid_derivative(z1)
# 입력층 -> 은닉층 가중치 및 편향 업데이트
dL_dW1 = np.dot(X.T, dL_dz1)
dL_db1 = np.sum(dL_dz1, axis=0, keepdims=True)
# 가중치 및 편향 업데이트
W2 -= learning_rate * dL_dW2
b2 -= learning_rate * dL_db2
W1 -= learning_rate * dL_dW1
b1 -= learning_rate * dL_db1
if epoch % 1000 == 0:
print(f'Epoch {epoch}, Loss: {loss_value}')
# 최종 예측 값 출력
print("Final predictions:")
print(a2)sigmoid 함수: 은닉층과 출력층에서 사용하는 활성화 함수.
순전파: 입력 데이터를 신경망을 통해 전달하여 예측값을 계산.
역전파: 출력과 실제 값의 차이로부터 가중치에 대한 기울기를 계산하고, 이를 사용해 가중치를 업데이트.
경사하강법: 학습률에 따라 가중치를 수정하여 손실을 줄여 나감.
이 코드는 XOR 문제를 해결하기 위한 간단한 신경망이며, 각 에포크(epoch)마다 가중치가 업데이트되어 손실(loss)이 감소한다.

- 다층신경망을 적용한 매출예측
import numpy as np
# ReLU 활성화 함수 정의
def relu(z):
return np.maximum(0, z)
# ReLU 미분 함수 (Backpropagation에서 사용)
def relu_derivative(z):
return np.where(z > 0, 1, 0)
# 손실 함수 (Mean Squared Error)
def compute_loss(Y, A):
m = Y.shape[1] # 샘플 수
loss = np.mean((Y - A) ** 2) # MSE 계산
return loss
# 가중치 및 편향 초기화 함수
def initialize_parameters(layer_dims):
np.random.seed(1)
parameters = {}
for l in range(1, len(layer_dims)):
parameters['W' + str(l)] = np.random.randn(layer_dims[l], layer_dims[l-1]) * 0.01
parameters['b' + str(l)] = np.zeros((layer_dims[l], 1))
return parameters
# 순전파 (Forward Propagation)
def forward_propagation(X, parameters):
cache = {}
# 첫 번째 은닉층
W1 = parameters['W1']
b1 = parameters['b1']
Z1 = np.dot(W1, X) + b1
A1 = relu(Z1)
# 두 번째 은닉층
W2 = parameters['W2']
b2 = parameters['b2']
Z2 = np.dot(W2, A1) + b2
A2 = relu(Z2)
# 출력층 (회귀 문제이므로 활성화 함수 없음)
W3 = parameters['W3']
b3 = parameters['b3']
Z3 = np.dot(W3, A2) + b3
A3 = Z3 # 출력층 활성화 함수는 사용하지 않음
# 캐시 저장 (역전파에서 사용)
cache['Z1'], cache['A1'] = Z1, A1
cache['Z2'], cache['A2'] = Z2, A2
cache['Z3'], cache['A3'] = Z3, A3
return A3, cache
# 역전파 (Backward Propagation)
def backward_propagation(X, Y, parameters, cache):
m = X.shape[1] # 샘플 수
grads = {}
# 출력층 오차
A3 = cache['A3']
dZ3 = A3 - Y
grads['dW3'] = np.dot(dZ3, cache['A2'].T) / m
grads['db3'] = np.sum(dZ3, axis=1, keepdims=True) / m
# 두 번째 은닉층 오차
dA2 = np.dot(parameters['W3'].T, dZ3)
dZ2 = dA2 * relu_derivative(cache['Z2'])
grads['dW2'] = np.dot(dZ2, cache['A1'].T) / m
grads['db2'] = np.sum(dZ2, axis=1, keepdims=True) / m
# 첫 번째 은닉층 오차
dA1 = np.dot(parameters['W2'].T, dZ2)
dZ1 = dA1 * relu_derivative(cache['Z1'])
grads['dW1'] = np.dot(dZ1, X.T) / m
grads['db1'] = np.sum(dZ1, axis=1, keepdims=True) / m
return grads
# 파라미터 업데이트 (경사 하강법)
def update_parameters(parameters, grads, learning_rate):
for l in range(1, len(parameters) // 2 + 1):
parameters['W' + str(l)] -= learning_rate * grads['dW' + str(l)]
parameters['b' + str(l)] -= learning_rate * grads['db' + str(l)]
return parameters
# 학습 데이터 생성 (하드코딩된 연도별 매출 데이터)
X_train = np.array([[2017, 2018, 2019, 2020, 2021]]) # 연도
Y_train = np.array([[100, 150, 200, 250, 300]]) # 해당 연도의 매출
# 데이터 정규화
X_train = X_train / 2021 # 연도를 최대값으로 나누어 정규화
Y_train = Y_train / 300 # 매출도 최대값으로 나누어 정규화
# 레이어 구성 (입력층 1, 은닉층 2개, 출력층 1개)
layer_dims = [1, 5, 3, 1]
# 파라미터 초기화
parameters = initialize_parameters(layer_dims)
# 학습 하이퍼파라미터
learning_rate = 0.01
num_iterations = 10000
# 학습 과정
for i in range(num_iterations):
# 순전파
A3, cache = forward_propagation(X_train, parameters)
# 손실 계산
loss = compute_loss(Y_train, A3)
# 역전파
grads = backward_propagation(X_train, Y_train, parameters, cache)
# 파라미터 업데이트
parameters = update_parameters(parameters, grads, learning_rate)
# 1000번마다 손실 출력
if i % 1000 == 0:
print(f"Iteration {i}, Loss: {loss:.4f}")
# 테스트 데이터 예측
X_test = np.array([[2022]]) # 테스트 데이터 (2022년)
X_test = X_test / 2021 # 정규화
# 순전파로 예측
A3_test, _ = forward_propagation(X_test, parameters)
# 예측 결과 출력 (2022년 매출 예측)
print("2022년 매출 예측 (원래 값):", A3_test * 300) # 원래 단위로 변환
심층 신경망(Deep Neural Network, DNN)
- 구조: 심층 신경망은 여러 개의 은닉층을 가지는 신경망을 의미한다. 일반적으로 3개 이상의 은닉층을 가진 신경망을 심층 신경망이라고 한다.
- 특징:
- 은닉층의 수가 많아질수록 데이터의 복잡한 패턴을 더 잘 학습할 수 있다.
- 각 은닉층은 이전 층에서 입력받은 신호를 비선형 변환을 통해 다음 층으로 전달하면서 데이터를 점점 더 추상적인 수준으로 표현한다.
- 딥러닝(Deep Learning)이라는 용어는 심층 신경망을 이용한 학습 방법을 가리키며, 심층 신경망은 이미지 처리(CNN, Convolutional Neural Network), 시계열 데이터 처리(RNN, Recurrent Neural Network), 자연어 처리 등에 널리 사용된다.
- 장점:
- 복잡하고 비선형적인 데이터 패턴을 학습할 수 있다.
- 다층 구조를 통해 데이터의 더 높은 차원에서 의미 있는 특징(feature)을 추출할 수 있다.
- 이미지 인식, 음성 인식, 자연어 처리 등의 복잡한 문제를 해결하는 데 적합.
- 단점:
- 계산 비용이 매우 높고, 학습 시간이 오래 걸린다.
- 많은 데이터와 높은 계산 능력을 필요로 한다.
- 과적합(overfitting)의 위험이 있어 적절한 규제 기법(regularization)이 필요하다.
다층 신경망 기반 분류모델 연습
- 디렉토리 구조 (구글 코랩에서)

이미지 데이터를 받아 구글 colab에서 개 이미지는 개 폴더에 고양이 이미지는 고양이 폴더에 넣는다.
- 학습모델 만드는 코드
# tensorflow 통해 개 고양이 이미지 분류 (다층신경망 기반 분류모델 연습)
# 우선 학습모델 만드는 코드
import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Flatten
from tensorflow.keras.preprocessing.image import ImageDataGenerator
import os
# 경로 설정
base_dir = '/content/data' # 데이터 경로 설정
# 이미지 로드 및 전처리 (데이터 증강 없이)
train_datagen = ImageDataGenerator(
rescale=1./255, # 픽셀 값을 0-1 사이로 정규화
validation_split=0.2 # 데이터의 20%를 검증용으로 분리
)
# 학습 데이터 로드
train_generator = train_datagen.flow_from_directory(
base_dir, # 데이터가 저장된 디렉토리
target_size=(64, 64), # 이미지 크기 조정
batch_size=32, # 배치 크기
class_mode='binary', # 이진 분류
subset='training' # 학습 데이터
)
# 검증 데이터 로드
validation_generator = train_datagen.flow_from_directory(
base_dir, # 데이터가 저장된 디렉토리
target_size=(64, 64), # 이미지 크기 조정
batch_size=32, # 배치 크기
class_mode='binary', # 이진 분류
subset='validation' # 검증 데이터
)
# 다층 신경망 모델 구성
model = Sequential()
# 입력 데이터를 평탄화 (Flatten)하여 1차원으로 변환
model.add(Flatten(input_shape=(64, 64, 3))) # 이미지 크기가 64x64, RGB 채널 3개
# 은닉층 (뉴런 128개)
model.add(Dense(128, activation='relu'))
# 은닉층 (뉴런 64개)
model.add(Dense(64, activation='relu'))
# 출력층 (뉴런 1개, 시그모이드 활성화 함수 사용)
model.add(Dense(1, activation='sigmoid'))
# 모델 컴파일 (이진 분류, 손실 함수로 binary_crossentropy 사용)
model.compile(optimizer='adam',
loss='binary_crossentropy',
metrics=['accuracy'])
# 모델 학습
history = model.fit(
train_generator,
steps_per_epoch=train_generator.samples // train_generator.batch_size,
epochs=100, # 에포크 수를 설정하여 학습 반복
validation_data=validation_generator,
validation_steps=validation_generator.samples // validation_generator.batch_size
)
# 모델 저장
model.save('dog_cat_classifier_mlp.h5')
# 테스트용 데이터로 예측
test_loss, test_acc = model.evaluate(validation_generator)
print(f"테스트 정확도: {test_acc}")※ Dense 층은 입력과 출력에 완전연결(Fully connected)된 층으로서 인공신경망에서 기본 층으로 사용된다.
- 위의 학습모델을 이용한 테스트 코드
import tensorflow as tf
from tensorflow.keras.models import load_model
from tensorflow.keras.preprocessing import image
import numpy as np
# 모델 로드
model = load_model('dog_cat_classifier_mlp.h5')
# 테스트 이미지 경로
test_image_path = '/content/data/dog/dog (1).jpeg' # 테스트 이미지 경로를 지정
# 테스트 이미지 로드 및 전처리
def load_and_preprocess_image(img_path):
# 이미지를 64x64 크기로 로드하고 RGB로 변환
img = image.load_img(img_path, target_size=(64, 64))
# 이미지를 numpy 배열로 변환
img_array = image.img_to_array(img)
# 차원을 추가하여 (1, 64, 64, 3) 형태로 만듦 (모델 입력 차원과 맞춤)
img_array = np.expand_dims(img_array, axis=0)
# 이미지의 픽셀 값을 0-1 사이로 정규화
img_array /= 255.0
return img_array
# 이미지 로드 및 전처리
test_image = load_and_preprocess_image(test_image_path)
# 분류 예측
prediction = model.predict(test_image)
# 예측 결과 해석
if prediction[0] > 0.5:
print("이 이미지는 개일 가능성이 높습니다.")
else:
print("이 이미지는 고양이일 가능성이 높습니다.")
코드를 돌리면 loss가 Epoch 할때마다 줄어들어야 하는데 뭔가 좀 이상하다.

코드를 돌린 결과 정확도가 좋지 않았다.
학습이 잘 안됐을 경우에는 Learning Rate, Epoch, Batch Size를 고쳐보는 것이 좋다.
Epoch 일단 고쳐보는게 간단하긴 함.
혹은 양질의 데이터(사진)을 늘리는게 도움이 된다.
accuracy를 향상시키는게 매우 중요하다.
경제지수를 반영해서 다층신경망으로 SK하이닉스 종가 예측
# sk 하이닉스 종목 종가 예측
import pandas as pd
import numpy as np
import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import r2_score
from pykrx import stock
import FinanceDataReader as fdr
# 1. SK하이닉스 종가 데이터 가져오기
df = stock.get_market_ohlcv("20240301", "20250312", "000660")
df.reset_index(inplace=True)
# 2. 날짜 변환 (연도, 월, 일)
df['Year'] = df['날짜'].dt.year
df['Month'] = df['날짜'].dt.month
df['Day'] = df['날짜'].dt.day
# 3. 주요 경제 지수 데이터 가져오기 (KOSPI, KOSDAQ, KOSPI200, USD/KRW 환율)
kospi = fdr.DataReader('KS11', '2024-01-01', '2024-12-31')['Close']
kosdaq = fdr.DataReader('KQ11', '2024-01-01', '2024-12-31')['Close']
kospi200 = fdr.DataReader('KS200', '2024-01-01', '2024-12-31')['Close']
usd_krw = fdr.DataReader('USD/KRW', '2024-01-01', '2024-12-31')['Close']
# 4. 경제 지수 병합
df = df.set_index('날짜')
df['KOSPI'] = kospi
df['KOSDAQ'] = kosdaq
df['KOSPI200'] = kospi200
df['USD_KRW'] = usd_krw
df.dropna(inplace=True) # NaN 데이터 제거
# 5. 데이터 정리 및 입력 변수 설정 (KRX300 삭제)
df.reset_index(inplace=True)
df = df[['Year', 'Month', 'Day', '거래량', 'KOSPI', 'KOSDAQ', 'KOSPI200', 'USD_KRW', '종가']]
# 6. 입력 변수(X)와 출력 변수(y) 정의 (KRX300 삭제)
X = df[['Year', 'Month', 'Day', '거래량', 'KOSPI', 'KOSDAQ', 'KOSPI200', 'USD_KRW']].values
y = df['종가'].values
# 7. 데이터 정규화
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
# 8. 다층 신경망 모델 정의
model = Sequential([
Dense(128, activation='relu', input_shape=(X_scaled.shape[1],)),
Dense(64, activation='relu'),
Dense(32, activation='relu'),
Dense(1) # 출력층 (종가 예측)
])
# 9. 모델 컴파일 및 학습
model.compile(optimizer=tf.keras.optimizers.Adam(learning_rate=0.001), loss='mean_squared_error')
model.fit(X_scaled, y, epochs=500, batch_size=10, verbose=1)
# 10. 모델 성능 평가 (R² 값 계산)
y_pred = model.predict(X_scaled)
r2 = r2_score(y, y_pred)
print(f"R² 값: {r2:.4f}")
# 11. 특정 날짜의 SK하이닉스 종가 예측 함수 (KRX300 삭제)
def predict_stock_price(year, month, day, volume, kospi, kosdaq, kospi200, usd_krw):
input_data = np.array([[year, month, day, volume, kospi, kosdaq, kospi200, usd_krw]])
input_data_scaled = scaler.transform(input_data)
predicted_price = model.predict(input_data_scaled)
return predicted_price[0][0]
# 12. 2025년 3월 12일 SK하이닉스 종가 예측 (거래량 1,500만, 예측된 경제 지수 사용)
kospi_2025 = 3100 # 예측된 KOSPI 지수
kosdaq_2025 = 950 # 예측된 KOSDAQ 지수
kospi200_2025 = 430 # 예측된 KOSPI200 지수
usd_krw_2025 = 1300 # 예측된 USD/KRW 환율
predicted_price_2025 = predict_stock_price(2025, 3, 12, 15000000, kospi_2025, kosdaq_2025, kospi200_2025, usd_krw_2025)
print(f"2025년 3월 12일 SK하이닉스 종가 예측: {predicted_price_2025:.2f} 원")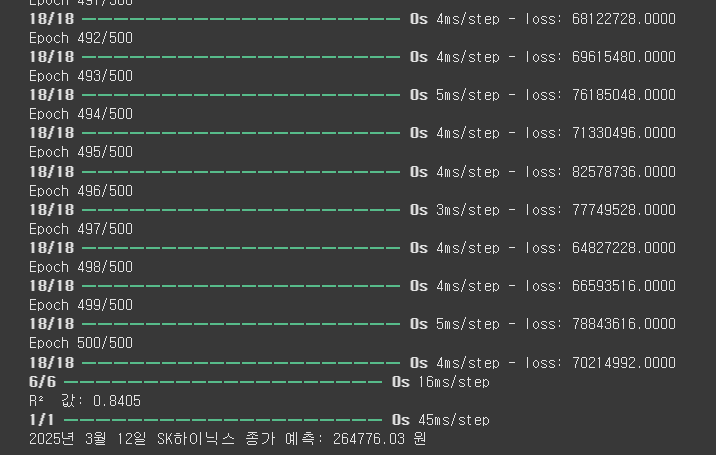
epoch할때마다 loss(손실)이 정상적으로 줄어드는걸 볼 수 있음.

2025년 3월 12일 SK하이닉스 종가를 예측해보았는데 실제 종가와 매우 달랐다. (실제종가 198,900원) 주가가 변동하는 이유는 여러가지가 있기 때문에 맞추기 힘들다. 맞출 수 있었으면 AI전문가들 다 부자되지 않았을까..
신경망 학습을 위한 Hyper parameter 요약
| 개념 | 정의 | 역할 |
| Epoch (에포크) | 전체 데이터셋을 신경망에 한 번 완전히 통과시켜 학습하는 과정 | 에포크 수가 많으면 더 많은 학습을 가능하게 하지만, 과적합 위험이 있음 |
| Batch Size (배치 크기) | 전체 데이터를 일정 크기의 묶음으로 나누어 학습하는 단위 | 크기에 따라 메모리 사용량과 학습 안정성에 영향을 줌 |
| Learning Rate (학습률) | 한 번 학습할 때 가중치를 얼마나 조정할지 결정하는 값 | 값이 크면 빠르게 학습하지만 불안정, 작으면 안정적이지만 느림 |
학습이 잘 안됐을 때 위 3개를 고쳐보는 것이 좋음. (혹은 양질의 데이터 늘리기)
- Google teachable machine을 이용해 만든 keras model로 GCP VM에서 Python과 Tensorflow를 이용해 동작 실습 하기.
티쳐블 머신에 접속해서 사진들을 업로드하고 모델 내보내기 클릭. 모델 변환유형은 Keras로 하고 모델을 다운로드.

위 zip파일은 티쳐블머신에서 다운받은 keras_model.h5 과 labels.txt가 포함된 파일이다.
html파일은 templates에, 나머지 파일은 templates의 상위폴더에 넣어서 python3 app.py 명령어로 실행한다.
(파일 업로드 - 파일질라 이용).
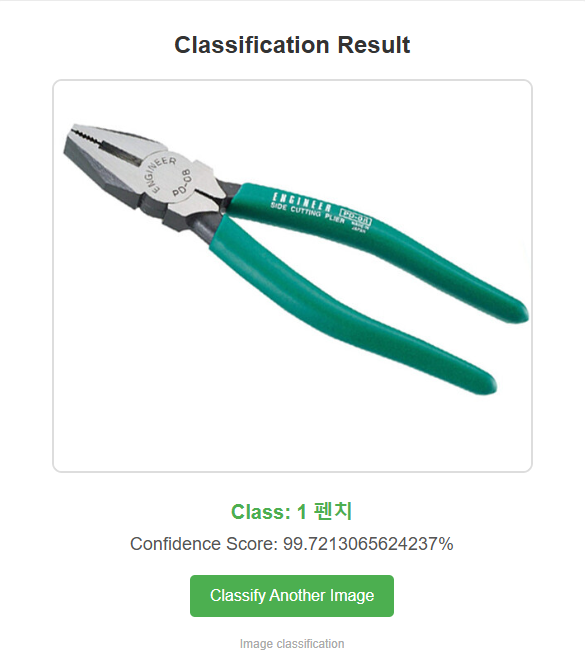
http://외부ip주소:포트번호 들어가서 사진들을 넣어보고 잘 분류가 되는지 확인한다.
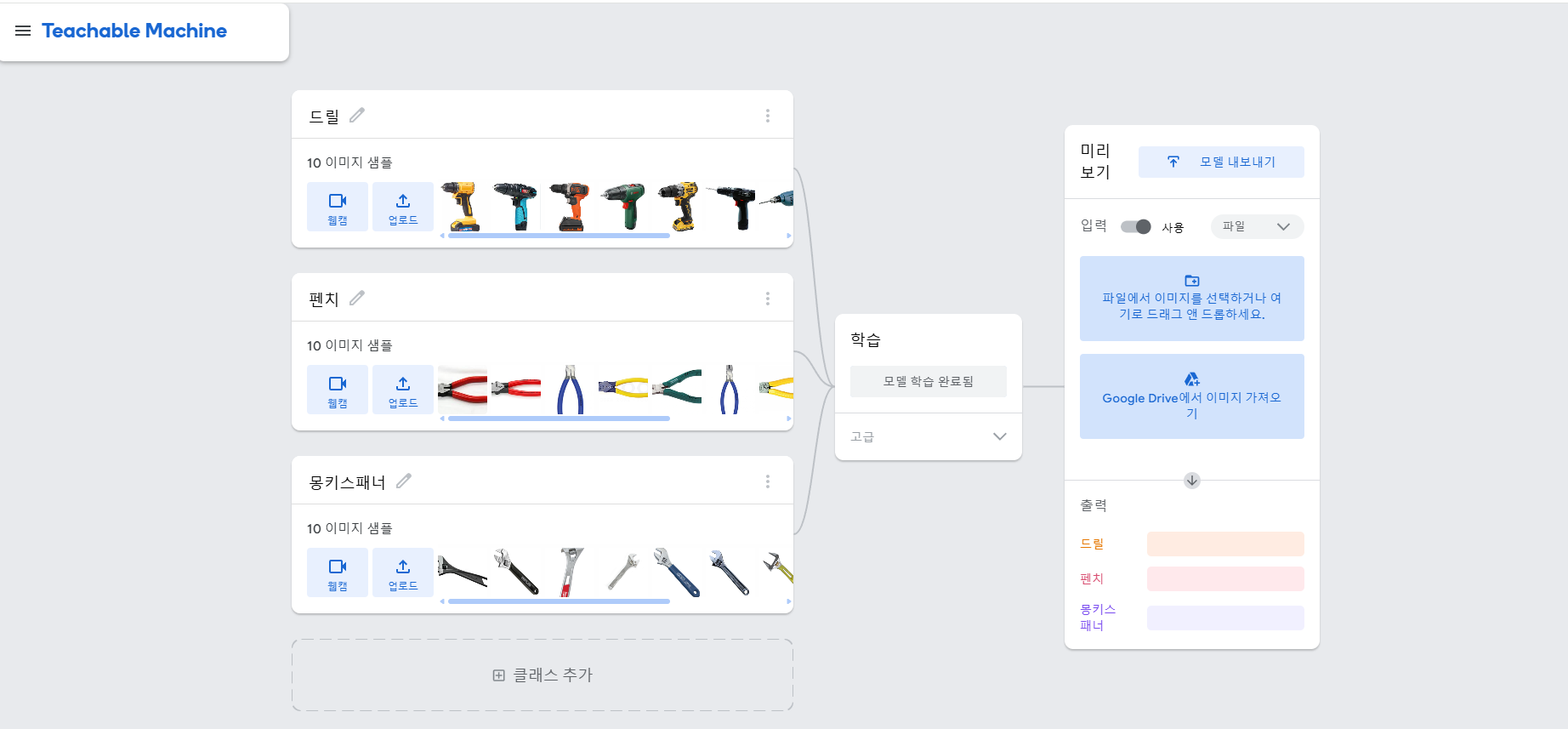
티쳐블머신은 CNN알고리즘 기반이기 때문에 성능이 좋아서 분류가 잘 된다.


공구를 분류하는 것도 사진들을 모아서 실습해보았다.
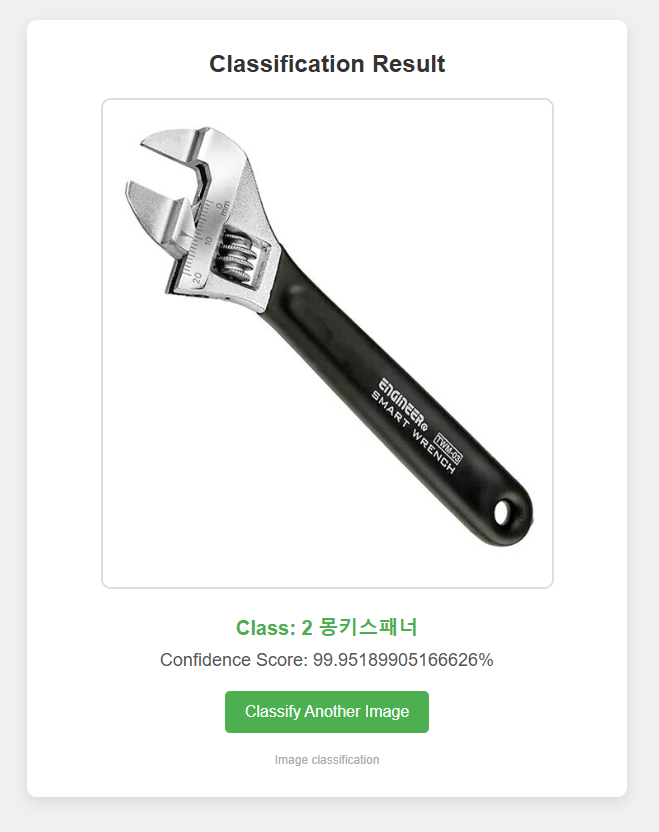

복습
# 결정 트리를 활용해 Iris 데이터셋을 분류하는 과정
# 결정트리구현 (복습)
from sklearn.tree import DecisionTreeClassifier
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
# 데이터 로드
iris = load_iris()
X_train, X_test, y_train, y_test = train_test_split(iris.data, iris.target, test_size=0.2, random_state=42)
# 결정 트리 모델 학습
clf = DecisionTreeClassifier(max_depth=3, random_state=42)
clf.fit(X_train, y_train)
# 예측 및 정확도 평가
y_pred = clf.predict(X_test)
print("정확도:", accuracy_score(y_test, y_pred))
Iris 데이터셋 : 꽃받침 길이/너비, 꽃잎 길이/너비를 이용해 3가지 붓꽃 품종을 분류하는 데이터
데이터 분할 : 80% 학습, 20% 테스트
결정 트리 모델 학습 : 트리를 사용해 데이터를 분류, max_depth=3으로 과적합 방지
예측 및 평가 : accuracy_score()로 모델 성능 평가
# 랜덤포레스트 데이터 개선해서 결정계수 좋게 나오게 하기
- 기존의 결정계수 나쁜 코드
# 랜덤 포레스트를 이용한 그로스 마케팅 예측 (결정계수 개선하기 -전단계)
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import mean_absolute_error, mean_squared_error, r2_score
# 1. 샘플 데이터 생성 (고객 행동 데이터)
np.random.seed(42)
num_customers = 200
data = pd.DataFrame({
'Customer_ID': range(1, num_customers + 1),
'Previous_Spending': np.random.randint(50, 500, size=num_customers), # 이전 총 구매 금액 ($)
'Visit_Frequency': np.random.randint(1, 20, size=num_customers), # 웹사이트 방문 빈도 (월 단위)
'Average_Order_Value': np.random.randint(10, 200, size=num_customers), # 평균 주문 금액 ($)
'Discount_Used': np.random.choice([0, 1], size=num_customers), # 할인 사용 여부 (0: 사용 안 함, 1: 사용)
'Future_Spending': np.random.randint(50, 600, size=num_customers) # 향후 한 달 동안의 예상 지출 ($)
})
# 2. 독립 변수(X)와 종속 변수(y) 설정
X = data[['Previous_Spending', 'Visit_Frequency', 'Average_Order_Value', 'Discount_Used']]
y = data['Future_Spending']
# 3. 훈련 데이터와 테스트 데이터 분리
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 4. 랜덤 포레스트 회귀 모델 학습
model = RandomForestRegressor(n_estimators=100, random_state=42)
model.fit(X_train, y_train)
# 5. 예측 수행
y_pred = model.predict(X_test)
# 6. 모델 성능 평가
mae = mean_absolute_error(y_test, y_pred)
mse = mean_squared_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)
print(f"Mean Absolute Error (MAE): {mae:.2f}")
print(f"Mean Squared Error (MSE): {mse:.2f}")
print(f"R² Score: {r2:.2f}")
# 7. 예측 결과 시각화
plt.figure(figsize=(8, 5))
plt.scatter(y_test, y_pred, alpha=0.7)
plt.xlabel("Actual Spending")
plt.ylabel("Predicted Spending")
plt.title("Actual vs Predicted Future Spending")
plt.plot([50, 600], [50, 600], color="red", linestyle="dashed") # y=x 선
plt.show()
- 결정계수 개선한 코드
# 랜덤 포레스트를 이용한 그로스 마케팅 예측 (결정계수 개선)
import seaborn as sns
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import mean_absolute_error, mean_squared_error, r2_score
# 1. 샘플 데이터 생성 (고객 행동 데이터)
np.random.seed(42)
num_customers = 200
data = pd.DataFrame({
'Customer_ID': range(1, num_customers + 1),
'Previous_Spending': np.random.randint(50, 500, size=num_customers), # 이전 총 구매 금액 ($)
'Visit_Frequency': np.random.randint(1, 20, size=num_customers), # 웹사이트 방문 빈도 (월 단위)
'Average_Order_Value': np.random.randint(10, 200, size=num_customers), # 평균 주문 금액 ($)
'Discount_Used': np.random.choice([0, 1], size=num_customers), # 할인 사용 여부 (0: 사용 안 함, 1: 사용)
'Future_Spending': np.random.randint(50, 600, size=num_customers) # 향후 한 달 동안의 예상 지출 ($)
})
# 2. 데이터 변환 및 새로운 변수 추가
data['Log_Previous_Spending'] = np.log1p(data['Previous_Spending'])
data['Log_Future_Spending'] = np.log1p(data['Future_Spending'])
data['Discount_Usage_Rate'] = data['Discount_Used'] / (data['Visit_Frequency'] + 1)
data['Spending_Change'] = data['Future_Spending'] - data['Previous_Spending']
# 3. 이상치 제거 (IQR 방법)
Q1 = data['Future_Spending'].quantile(0.25)
Q3 = data['Future_Spending'].quantile(0.75)
IQR = Q3 - Q1
data = data[(data['Future_Spending'] >= (Q1 - 1.5 * IQR)) & (data['Future_Spending'] <= (Q3 + 1.5 * IQR))]
# 4. 독립 변수(X)와 종속 변수(y) 설정
X = data[['Log_Previous_Spending', 'Visit_Frequency', 'Average_Order_Value', 'Discount_Used', 'Discount_Usage_Rate', 'Spending_Change']]
y = data['Log_Future_Spending'] # 로그 변환된 값 사용
# 5. 훈련 데이터와 테스트 데이터 분리
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 6. 랜덤 포레스트 회귀 모델 학습 (하이퍼파라미터 조정)
model = RandomForestRegressor(n_estimators=200, max_depth=10, min_samples_split=5, min_samples_leaf=3, random_state=42)
model.fit(X_train, y_train)
# 7. 예측 수행
y_pred = model.predict(X_test)
# 8. 원래 스케일로 변환 (지수 변환)
y_test_exp = np.expm1(y_test)
y_pred_exp = np.expm1(y_pred)
# 9. 모델 성능 평가
mae = mean_absolute_error(y_test_exp, y_pred_exp)
mse = mean_squared_error(y_test_exp, y_pred_exp)
r2 = r2_score(y_test_exp, y_pred_exp)
print(f"Mean Absolute Error (MAE): {mae:.2f}")
print(f"Mean Squared Error (MSE): {mse:.2f}")
print(f"R² Score: {r2:.2f}")
# 10. 예측 결과 시각화
plt.figure(figsize=(8, 5))
plt.scatter(y_test_exp, y_pred_exp, alpha=0.7)
plt.xlabel("Actual Spending")
plt.ylabel("Predicted Spending")
plt.title("Actual vs Predicted Future Spending")
plt.plot([50, 600], [50, 600], color="red", linestyle="dashed") # y=x 선
plt.show()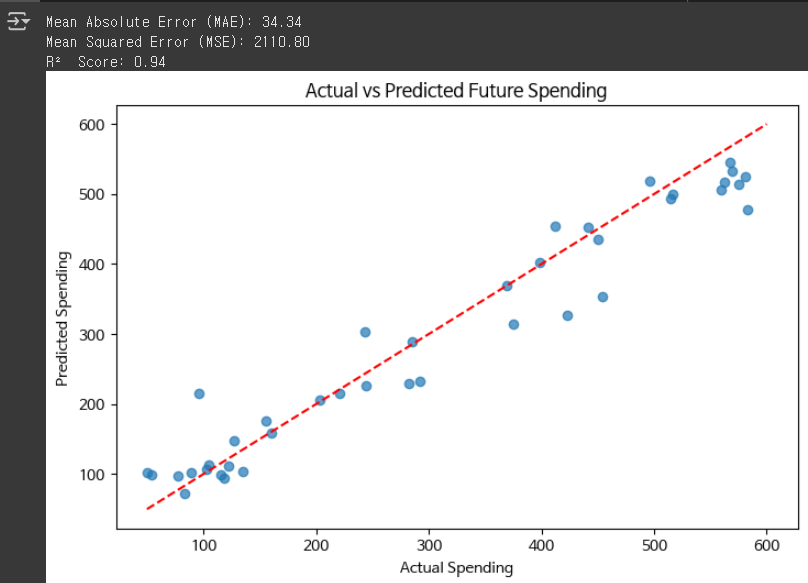
여기서 데이터샘플을 100개로 늘리면 결정계수가 아주좋아짐. 0.99가 된다.
※ 결정계수(R² score)가 개선된 이유
1) 데이터 변환 및 새로운 변수 추가
추가된 변화
- Log_Previous_Spending = np.log1p(data['Previous_Spending'])
- Log_Future_Spending = np.log1p(data['Future_Spending'])
- Discount_Usage_Rate = data['Discount_Used'] / (data['Visit_Frequency'] + 1)
- Spending_Change = data['Future_Spending'] - data['Previous_Spending']
효과
- 로그 변환(log1p) 적용
- Previous_Spending(이전 지출)과 Future_Spending(미래 지출)에 로그 변환을 적용했다.
- 지출 데이터는 일반적으로 오른쪽으로 치우친 분포(스큐됨) 을 가지기 때문에, 로그 변환을 하면 분포가 더 정규분포에 가까워져서 예측 성능이 좋아짐.
- 할인 사용률 변수(Discount_Usage_Rate) 추가
- 기존에는 할인 여부(0 또는 1)만 사용했는데, Discount_Usage_Rate = 할인 사용 여부 / (방문 빈도 + 1) 를 추가하면서 할인을 얼마나 자주 활용하는지를 반영했다.
- 단순한 0/1보다 연속적인 값이 들어가면 모델이 패턴을 더 잘 학습할 수 있음.
- 지출 변화량(Spending_Change) 추가
- Future_Spending - Previous_Spending 변수를 만들어서 소비 패턴의 변화를 반영했음.
- 지출이 증가하는 고객과 감소하는 고객을 구분할 수 있어서 더 좋은 예측이 가능해졌다.
2) 이상치 제거 (IQR 방법)
추가된 코드
Q1 = data['Future_Spending'].quantile(0.25)
Q3 = data['Future_Spending'].quantile(0.75)
IQR = Q3 - Q1
data = data[(data['Future_Spending'] >= (Q1 - 1.5 * IQR)) & (data['Future_Spending'] <= (Q3 + 1.5 * IQR))]- 기존 코드에서는 이상치를 제거하지 않았음.
- 이상치(극단적인 값)가 있으면 랜덤 포레스트 모델이 잘못된 패턴을 학습할 수 있는데, 이를 제거하면 일반적인 패턴을 더 잘 학습할 수 있다.
- 특히 Future_Spending 값이 너무 크거나 작은 데이터가 모델에 영향을 미치지 않도록 하였음.
3) 하이퍼파라미터 튜닝
변경된 부분
model = RandomForestRegressor(n_estimators=200, max_depth=10, min_samples_split=5, min_samples_leaf=3, random_state=42)- n_estimators=100 → 200
- 트리를 2배 늘려서 예측의 안정성을 높였다.
- max_depth=None(기본값) → 10
- 트리의 깊이를 제한해서 과적합을 방지했음.
- min_samples_split=2(기본값) → 5
- 노드를 분할할 최소 샘플 개수를 증가시켜서 너무 세밀한 분할을 방지했다.
- min_samples_leaf=1(기본값) → 3
- 리프 노드에 최소 3개 이상의 샘플이 있도록 해서 일반화 성능을 높였다.
효과
- 트리 개수를 늘리고 과적합을 방지하는 설정을 추가해서 모델이 좀 더 일반화된 패턴을 학습하게 되었음.
- 원래는 훈련 데이터에 너무 맞춰져서 테스트 데이터에서 성능이 안 나올 수도 있었는데, 이걸 개선한 것.
4) 로그 변환된 값 예측 후 원래 스케일로 변환
추가된 부분
y_test_exp = np.expm1(y_test)
y_pred_exp = np.expm1(y_pred)- 로그 변환한 y_train을 학습했기 때문에, 예측 결과도 로그 스케일.
- np.expm1()를 사용해서 다시 원래 스케일로 변환했다.
효과
- 로그 변환한 값을 사용하면 예측 오차가 줄어들지만, 최종 결과를 원래 단위로 되돌려야 함.
- 원래 스케일로 변환해야 해석이 가능하고, 성능 평가가 정확해진다.
* 정리 *
- 로그 변환 적용 → 데이터 분포 정규화 → 예측 성능 향상
- 새로운 변수 추가(할인 사용률, 지출 변화량) → 추가적인 정보 학습 가능
- 이상치 제거 → 극단적인 데이터로 인한 왜곡 방지
- 하이퍼파라미터 튜닝 → 과적합 방지 및 일반화 성능 개선
- 로그 변환된 값을 다시 원래 스케일로 변환 → 평가 정확도 증가
특징 엔지니어링에 대해서 더욱 깊은 복습이 필요하다.
# K평균 군집화 활용 - 고객 세분화
# 예제 1: 고객 세분화
from sklearn.preprocessing import StandardScaler
import pandas as pd
# 샘플 고객 데이터 생성
data = {
"Annual_Income": [15, 16, 17, 50, 52, 53, 100, 105, 110],
"Spending_Score": [39, 40, 45, 60, 65, 70, 15, 18, 20]
}
df = pd.DataFrame(data)
# 데이터 정규화
scaler = StandardScaler()
scaled_data = scaler.fit_transform(df)
# K-평균 군집화 수행
kmeans = KMeans(n_clusters=3, random_state=42)
df["Cluster"] = kmeans.fit_predict(scaled_data)
print(df)
정규화 때문에 "소득"과 "소비 점수"가 균형 잡힌 영향을 줬고, K-Means가 이를 기반으로 군집을 찾음.
K-Means는 거리 기반 알고리즘이라서 비슷한 위치에 있는 데이터끼리 묶음.
결과적으로 (저소득-중간소비), (중소득-고소비), (고소득-저소비) 그룹으로 나눠짐.
# K평균 군집화 활용 - 이미지 색상 압축
# 예제 2: 이미지 색상 압축
from sklearn.cluster import KMeans
from skimage import io
import numpy as np
# 이미지 로드
image = io.imread("dog (12).jpeg")
pixels = image.reshape(-1, 3)
# K-평균 군집화 적용
kmeans = KMeans(n_clusters=16, random_state=42)
kmeans.fit(pixels)
compressed_pixels = kmeans.cluster_centers_[kmeans.labels_]
compressed_image = compressed_pixels.reshape(image.shape)
# 압축된 이미지 시각화
plt.figure(figsize=(10, 5))
plt.subplot(1, 2, 1)
plt.imshow(image)
plt.title("Original Image")
plt.axis("off")
plt.subplot(1, 2, 2)
plt.imshow(compressed_image.astype(np.uint8))
plt.title("Compressed Image (16 Colors)")
plt.axis("off")
plt.show()
이미지의 색상을 줄이는 데 K-평균 군집화를 사용할 수 있다. 이 코드는 K-평균 군집화를 사용하여 원본 이미지의 색상을 16개의 주요 색상으로 줄였다.
# K평균 군집화 활용 - 이상치 탐지
# 예제 3: 이상치 탐지
import numpy as np
# 샘플 거래 데이터 생성
transactions = np.array([
[50, 1], [60, 1], [55, 2], [700, 5], [58, 2], [62, 1], [750, 5], [65, 2]
])
# K-평균 군집화 적용
kmeans = KMeans(n_clusters=2, random_state=42)
labels = kmeans.fit_predict(transactions)
# 이상치 탐지
outliers = transactions[labels == labels.max()]
print("Detected Outliers:", outliers)K-평균 군집화를 사용하여 정상적인 데이터 포인트와 이상치를 구별할 수 있다.
# K-평균 군집화에서 최적의 K값을 찾는 방법
K-평균(K-Means) 알고리즘은 군집의 개수(K)를 사용자가 미리 설정해야 한다는 단점이 있다. 따라서 최적의 K값을 찾기 위해 엘보우(Elbow) 기법과 실루엣(Silhouette) 점수를 활용할 수 있다.
| 방법 | 설명 | 최적 K값 찾는 방법 |
| 엘보우 기법 | 군집 내 변동 값(Inertia, WCSS)을 계산하여, 그래프의 기울기가 급격히 완만해지는 지점(Knee Point)을 최적 K값으로 선택 | 기울기가 크게 꺾이는 지점을 찾음 |
| 실루엣 점수 | 각 데이터 포인트가 자신의 군집과 얼마나 밀접하게 묶여 있으며, 다른 군집과는 얼마나 분리되어 있는지를 측정 | 점수가 가장 높은 K값 선택 |
※ 엘보우 기법을 주로 많이 쓰며 실루엣 점수는 잘 쓰지 않는다.
# 엘보우 기법 / 실루엣점수 이용한 최적 K값 찾기
# 데이터 생성
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score
from sklearn.datasets import make_blobs
# 샘플 데이터 생성
np.random.seed(42)
X, _ = make_blobs(n_samples=300, centers=4, cluster_std=1.0, random_state=42)
# < 엘보우 기법을 이용한 최적 K값 찾기 >
# K 값별 관성(Inertia) 저장
inertia = []
k_range = range(1, 11)
for k in k_range:
kmeans = KMeans(n_clusters=k, random_state=42)
kmeans.fit(X)
inertia.append(kmeans.inertia_)
# 엘보우 차트 그리기
plt.figure(figsize=(8, 5))
plt.plot(k_range, inertia, marker='o')
plt.xlabel("Number of Clusters (K)")
plt.ylabel("Inertia")
plt.title("Elbow Method for Optimal K")
plt.xticks(k_range)
plt.show()
# < 실루엣점수 이용한 최적 K값 찾기 >
# K 값별 실루엣 점수 저장
silhouette_scores = []
for k in range(2, 11): # 실루엣 점수는 최소 2개 이상의 클러스터가 필요
kmeans = KMeans(n_clusters=k, random_state=42)
labels = kmeans.fit_predict(X)
silhouette_scores.append(silhouette_score(X, labels))
# 실루엣 점수 그래프 그리기
plt.figure(figsize=(8, 5))
plt.plot(range(2, 11), silhouette_scores, marker='o', color='red')
plt.xlabel("Number of Clusters (K)")
plt.ylabel("Silhouette Score")
plt.title("Silhouette Score for Optimal K")
plt.xticks(range(2, 11))
plt.show()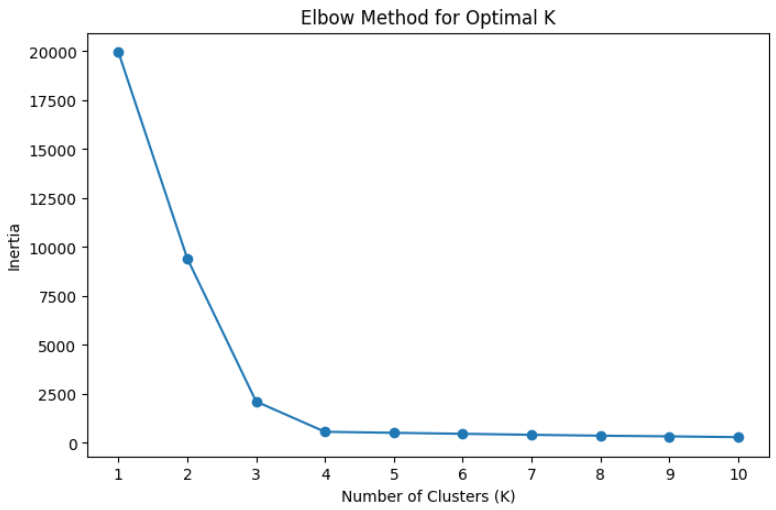

엘보우 기법을 통해 K값이 4에서 급격히 기울기가 완만해지는 것을 확인할 수 있다.
실루엣 점수를 보면, 가장 높은 점수를 갖는 4(K값)가 최적의 군집 개수로 판단할 수 있다.
'데이터 분석 part' 카테고리의 다른 글
| 계절성을 고려한 회귀분석 / 인공신경망의 기본 구조 & 역전파와 딥러닝 모델 학습 설명 (0) | 2025.03.17 |
|---|---|
| 차원축소, 계층적 군집 분석, 시계열데이터 예측 (회귀분석, 이동평균(MA), 지수 가중 이동 평균 (EMA)) / 마케팅 보고서 작성 연습 (1) | 2025.03.14 |
| k-NN 알고리즘, 서포트 벡터 머신(SVM), flask 웹실습 (2) | 2025.03.13 |
| 모델 성능 평가와 다중 분류 / 결정 트리의 기본 개념 / 랜덤 포레스트 개념과 구현 (0) | 2025.03.11 |
| 데이터 전처리, 특징 엔지니어링, 선형회귀, 로지스틱회귀 (0) | 2025.03.11 |