계절성을 고려한 회귀 분석 (Seasonal Regression Analysis)
기본 개념
회귀 분석은 종속 변수와 독립 변수 간의 관계를 분석하는 통계 기법이다. 그러나 많은 데이터는 시간에 따라 반복되는 계절적 패턴을 가지고 있다. 계절성을 고려하지 않으면 모델이 데이터의 패턴을 제대로 학습하지 못할 수 있다. (증감 영역을 잘 모르기 때문에)
( 예 : 아이스크림 판매량은 여름에 많고 겨울에 적음 / 난방기 판매량은 겨울에 많고 여름에 적음 / 월별 실업률, 주식 가격 등도 특정 시기에 따라 변할 수 있음 (경기 순환 등) )
계절성을 고려한 회귀 분석은 시간 요소(예: 월, 분기, 연도 등)를 독립 변수로 추가하여 계절적 변동을 반영하는 방법이다. 일반적으로 다음과 같은 방법을 사용한다.
1. 더미 변수(Dummy Variables) 추가 - 많이 쓰는거
- 더미 변수는 특정 범주형 데이터를 숫자로 변환하는 기법이다.
예를 들어, 월별 데이터를 분석할 때 1월~12월이 반복되는데, 이를 숫자로 직접 사용하면 의미가 없을 수 있다. 그래서 12개월 중 11개의 더미 변수를 만들어 특정 월의 영향을 반영할 수 있다.
※ 더미 변수를 12개가 아니라 11개만 쓰는 이유는 모든 더미 변수를 사용하면 다중 공선성 문제가 생기기 때문이다. 그래서 기준이 되는 '기준범주'(예: 1월)를 하나 정하고 나머지 11개만 더미 변수로 사용한다. 이렇게 하면 특정 달이 기준 달(1월)과 비교해서 얼마나 다른지를 확인할 수 있다.
※ '1월'을 기준으로 잡아, 월별 매출을 예측하려고 한다고 가정하면

여기서 X1, X2, ..., X11 은 특정 월에 해당하면 1, 아니면 0이 되는 더미 변수
B0은 1월의 평균값, B1, B2, B3..은 해당 월이 1월과 비교해서 얼마나 다른지
2. 푸리에 변환(Fourier Transformation) - 너무 루틴하다..
- 데이터가 특정 주기로 변하는 경우, 사인(sine)과 코사인(cosine) 함수를 사용해 계절성을 표현할 수 있다.
이 방법은 특히 '연속적인 계절성(예: 일별, 시간별 패턴이 있는 경우)'을 분석할 때 유용하다.
※ 예를 들어,

이렇게 하면 특정 주기의 패턴을 더 부드럽게 반영할 수 있다.
3. 이동 평균(Moving Average) 또는 지수 평활법(Exponential Smoothing) - 많이 쓰는거
- 계절성을 제거하거나 보정하는 방식으로 사용된다.
※ 이동 평균: 최근 몇 개의 데이터의 평균을 사용해서 변동을 완화함
※ 지수 평활법 : 최근 데이터에 더 큰 가중치를 주면서 변화하는 패턴을 반영함. 단순 이동평균보다 최근 변화에 더 민감하게 반응.
4. ARIMA 또는 SARIMA 모델 사용
- 시계열 데이터를 다룰 때 자주 사용되는 모델이며, 계절 조정이 포함된 SARIMA 모델은 계절성을 반영할 수 있다.
단순히 월별 영향을 반영하려면 더미 변수
주기적인 패턴을 반영하려면 푸리에 변환
데이터를 부드럽게 보정하려면 이동 평균 또는 지수 평활법
계절성을 자동으로 반영하려면 SARIMA 모델
- 계절성을 고려한 회귀 분석을 수행하는 예제 : 푸리에 변환
(주기적인 특성을 수학적으로 반영)
# 계절성을 고려한 회귀 분석을 수행하는 예제 (푸리에 변환)
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import statsmodels.api as sm
# 데이터 생성 (12개월 주기의 계절성을 가진 시계열 데이터)
np.random.seed(42)
months = np.arange(1, 25) # 2년 (24개월) 데이터
seasonal_effect = 10 * np.sin(2 * np.pi * months / 12) # 계절성 반영 (사인 함수)
trend = 0.5 * months # 증가하는 추세
noise = np.random.normal(0, 3, size=len(months)) # 랜덤 노이즈 추가
y = 50 + trend + seasonal_effect + noise # 최종 데이터
# 데이터프레임 생성
df = pd.DataFrame({"Month": months, "Sales": y})
df["Month_sin"] = np.sin(2 * np.pi * df["Month"] / 12) # 계절성을 위한 사인 변환
df["Month_cos"] = np.cos(2 * np.pi * df["Month"] / 12) # 계절성을 위한 코사인 변환
# 독립 변수 설정 (추세 + 계절성 반영)
X = df[["Month", "Month_sin", "Month_cos"]]
X = sm.add_constant(X) # 상수 추가 (절편)
# 회귀 분석 수행
model = sm.OLS(df["Sales"], X).fit()
# 결과 출력
print(model.summary())
# 예측 값 계산
df["Predicted"] = model.predict(X)
# 시각화
plt.figure(figsize=(10, 5))
plt.plot(df["Month"], df["Sales"], label="Actual Sales", marker='o')
plt.plot(df["Month"], df["Predicted"], label="Predicted Sales", linestyle="dashed", color="red")
plt.xlabel("Month")
plt.ylabel("Sales")
plt.title("Seasonal Regression Analysis")
plt.legend()
plt.grid()
plt.show()

- 시계열 데이터(판매량)에서 계절성과 추세를 반영하여 모델링.
- 계절성을 사인 함수와 코사인 함수를 사용해 학습 가능하게 변환. - 주기적 특성을 수학적으로 반영
- OLS(최소제곱법) 회귀 분석을 수행하여 계절적 패턴을 포함한 회귀 모델을 생성.
- 결과를 시각화하여 실제값과 예측값을 비교.
→ 이상적인 모양으로 나온다. 주기적 특성을 수학적으로 반영했기 때문에 잘 맞지 않는 경우 있음.
- 광고비와 프로모션이 매출에 미치는 영향분석 및 향후 매출 예측 - 푸리에 변환
- 주요 관심 대상 : 월별 광고비, 프로모션 여부, 트래픽(방문자 수)가 매출에 미치는 영향
- 계절성을 고려 : 특정계절 (ex.연말, 여름시즌)에 따른 매출 변동 반영
# 광고비와 프로모션이 매출에 미치는 영향분석 및 향후 매출 예측
# 데이터 생성 (계절성 반영)
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_absolute_error, r2_score
# 데이터 생성 설정
np.random.seed(42)
months = np.arange(1, 25) # 2년(24개월) 데이터
seasonal_effect = 20 * np.sin(2 * np.pi * months / 12) # 계절성 반영 (사인 함수)
trend = 2 * months # 증가하는 추세
noise = np.random.normal(0, 5, size=len(months)) # 랜덤 노이즈 추가
# 광고비, 트래픽, 프로모션 여부 설정
ad_spend = np.random.randint(50, 150, size=len(months)) # 광고비 (랜덤)
traffic = np.random.randint(1000, 5000, size=len(months)) # 방문자 수 (랜덤)
promotion = np.random.choice([0, 1], size=len(months), p=[0.7, 0.3]) # 프로모션 여부 (30% 확률)
# 최종 매출 데이터 생성 (광고비, 트래픽, 프로모션이 영향을 미침)
sales = 200 + (0.8 * ad_spend) + (0.05 * traffic) + (50 * promotion) + trend + seasonal_effect + noise
# 데이터프레임 생성
df = pd.DataFrame({
"Month": months,
"Ad_Spend": ad_spend,
"Traffic": traffic,
"Promotion": promotion,
"Sales": sales
})
# 계절성 반영을 위한 사인 및 코사인 추가
df["Month_sin"] = np.sin(2 * np.pi * df["Month"] / 12)
df["Month_cos"] = np.cos(2 * np.pi * df["Month"] / 12)
# 데이터 확인 (상위 5개 행 출력)
print(df.head())
# 위의 코드의 회귀분석 및 예측코드 (sklearn)
# 독립 변수 (계절성 반영)
X = df[["Ad_Spend", "Traffic", "Promotion", "Month_sin", "Month_cos"]]
y = df["Sales"]
# 모델 학습
model = LinearRegression()
model.fit(X, y)
# 예측 값 계산
df["Predicted_Sales"] = model.predict(X)
# 성능 평가
mae = mean_absolute_error(df["Sales"], df["Predicted_Sales"])
r2 = r2_score(df["Sales"], df["Predicted_Sales"])
print(f"Mean Absolute Error (MAE): {mae:.2f}")
print(f"R-squared (R²): {r2:.4f}")
# 결과 시각화
plt.figure(figsize=(10, 5))
plt.plot(df["Month"], df["Sales"], label="Actual Sales", marker='o')
plt.plot(df["Month"], df["Predicted_Sales"], label="Predicted Sales", linestyle="dashed", color="red")
plt.xlabel("Month")
plt.ylabel("Sales")
plt.title("Growth Marketing Regression Analysis (sklearn)")
plt.legend()
plt.grid()
plt.show()

- LinearRegression을 사용하여 광고비(Ad_Spend), 트래픽(Traffic), 프로모션(Promotion) 이 매출에 미치는 영향을 분석했다.
- 계절성 반영을 위해 Month_sin 및 Month_cos 변수를 추가하여 특정 월의 매출 변동을 모델이 학습하도록 함.
- Mean Absolute Error (MAE) 및 R² 점수를 확인하여 모델의 성능을 평가함.
- 그래프에서 실제 매출과 예측 매출의 차이를 시각적으로 확인할 수 있음.
→ 시도는 좋았으나 현상은 잘 안 맞고 '실제 데이터 중심'으로 하는게 효과적이다.
- Kpop 히트곡 주기를 반영한 화장품 브랜드 매출 예측 : 푸리에변환식을 사용해 주기를 반영한 코드.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_absolute_error, r2_score
# 1. 데이터 딕셔너리 정의 (Kpop 히트곡 주기성만 반영)
months = np.arange(1, 37) # 1~36개월 데이터
data = {
"Month": months,
"Sales": [
300, 320, 315, 330, 700, 340, 350, 330, 320, 310, 300, 295,
750, 360, 340, 330, 315, 300, 310, 305, 800, 350, 340, 320,
310, 300, 290, 280, 850, 360, 340, 330, 320, 310, 300, 295
],
"Ad_Spend": [
80, 100, 90, 110, 220, 120, 130, 110, 100, 90, 80, 75,
240, 140, 120, 110, 95, 80, 90, 85, 260, 130, 120, 100,
90, 80, 70, 60, 280, 140, 130, 110, 100, 90, 80, 75
],
"SNS_Viral_Score": [
1.5, 2, 1.8, 2.2, 8, 3, 3.5, 2.5, 2, 1.8, 1.5, 1,
9, 4, 3.5, 3, 2.5, 2, 1.5, 1.2, 10, 5, 4.5, 4,
3.5, 2.5, 2, 1.5, 12, 4, 3.8, 3.2, 2.7, 2.1, 1.8, 1.3
],
"Traffic": [
1200, 1300, 1250, 1350, 4200, 1400, 1450, 1300, 1200, 1150, 1100, 1050,
4300, 1500, 1400, 1300, 1200, 1100, 1050, 1000, 4400, 1600, 1500, 1400,
1300, 1200, 1100, 1050, 4600, 1550, 1400, 1300, 1200, 1150, 1100, 1050
],
"Promotion": [
0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0,
1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0,
0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0
]
}
# 2. Kpop 히트곡 주기를 반영한 주기 변수 추가 (9~12개월 주기, 평균 10.5개월)
data["Hit_Song_Sin"] = np.sin(2 * np.pi * data["Month"] / 10.5)
data["Hit_Song_Cos"] = np.cos(2 * np.pi * data["Month"] / 10.5)
# 3. 딕셔너리를 DataFrame으로 변환
df = pd.DataFrame(data)
# 4. 선형 회귀 분석을 위한 데이터 준비
X = df[["Month", "Ad_Spend", "SNS_Viral_Score", "Traffic", "Promotion", "Hit_Song_Sin", "Hit_Song_Cos"]]
y = df["Sales"]
# 5. 선형 회귀 모델 학습
model = LinearRegression()
model.fit(X, y)
# 6. 향후 12개월 예측 (37~48개월)
future_months = np.arange(37, 49)
future_data = {
"Month": future_months,
"Ad_Spend": [80, 100, 90, 110, 220, 120, 130, 110, 100, 90, 80, 75],
"SNS_Viral_Score": [1.5, 2, 1.8, 2.2, 8, 3, 3.5, 2.5, 2, 1.8, 1.5, 1],
"Traffic": [1200, 1300, 1250, 1350, 4200, 1400, 1450, 1300, 1200, 1150, 1100, 1050],
"Promotion": [0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0]
}
# 7. Kpop 히트곡 주기 반영 (향후 12개월)
future_data["Hit_Song_Sin"] = np.sin(2 * np.pi * future_data["Month"] / 10.5)
future_data["Hit_Song_Cos"] = np.cos(2 * np.pi * future_data["Month"] / 10.5)
# 8. DataFrame 변환 후 매출 예측
future_df = pd.DataFrame(future_data)
predicted_sales = model.predict(future_df)
# 9. 결과 시각화 (점선 연결)
plt.figure(figsize=(10, 5))
# 실제 데이터 점 (파란색)
plt.scatter(df["Month"], df["Sales"], color="blue", label="Actual Sales")
# 기존 데이터 + 예측 데이터를 하나의 배열로 연결
combined_months = np.concatenate((df["Month"], future_df["Month"]))
combined_sales = np.concatenate((model.predict(X), predicted_sales))
# 점선 스타일로 회귀선 표시
plt.plot(combined_months, combined_sales, color="red", linestyle="dashed", label="Regression Line")
# 예측값 (녹색 X)
plt.scatter(future_df["Month"], predicted_sales, color="green", marker="x", label="Predicted Sales")
plt.xlabel("Month")
plt.ylabel("Sales")
plt.title("Kpop 히트곡 주기를 반영한 화장품 브랜드 매출 예측")
plt.legend()
plt.show()
# 10. 성능 평가
y_pred = model.predict(X)
mae = mean_absolute_error(y, y_pred)
r2 = r2_score(y, y_pred)
print(f"Mean Absolute Error (MAE): {mae:.2f}")
print(f"R² Score: {r2:.2f}")
# 11. 향후 12개월 예측값 출력
future_df["Predicted_Sales"] = predicted_sales
print(future_df)
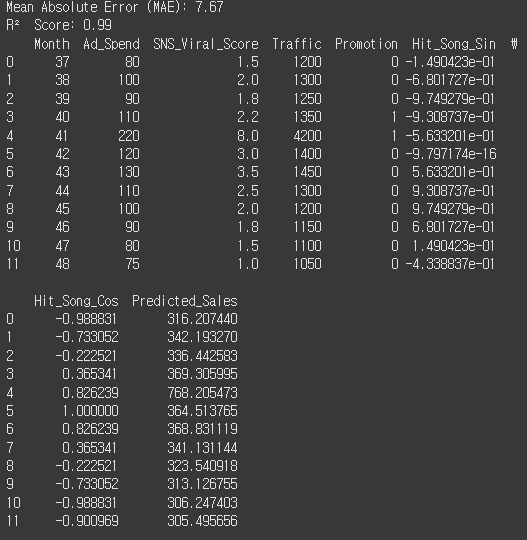
- 개인화된 추천 시스템 도입, 이메일 캠페인, 앱 내 알림 등이 월별 활성 사용자 수(MAU) 에 어떤 영향을 미쳤는지
# 개인화된 추천 시스템 도입, 이메일 캠페인, 앱 내 알림 등이 월별 활성 사용자 수(MAU) 에 어떤 영향을 미쳤는지
# < 데이터 생성 >
import numpy as np
import pandas as pd
# 데이터 생성 설정
np.random.seed(42)
months = np.arange(1, 13) # 12개월 데이터
base_users = 10000 # 기본 활성 사용자 수
# 마케팅 전략 효과 (가중치)
personalization_effect = 0.05 # 개인화 추천 시스템 도입 효과
email_campaign_effect = 0.03 # 이메일 캠페인 효과
in_app_notification_effect = 0.02 # 앱 내 알림 효과
# 각 전략의 실행 여부 (1: 실행, 0: 미실행)
personalization = np.array([0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]) # 3월부터 도입
email_campaign = np.array([0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1]) # 격월로 실행
in_app_notification = np.array([0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1]) # 5월부터 도입
# 월별 활성 사용자 수 계산
mau = base_users * (1 + personalization * personalization_effect +
email_campaign * email_campaign_effect +
in_app_notification * in_app_notification_effect)
# 노이즈 추가
noise = np.random.normal(0, 200, size=len(months))
mau = mau + noise
# 데이터프레임 생성
df = pd.DataFrame({
"Month": months,
"Personalization": personalization,
"Email_Campaign": email_campaign,
"In_App_Notification": in_app_notification,
"MAU": mau
})
# 데이터 확인
print(df)
# < 회귀분석 및 예측 코드 >
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_absolute_error, r2_score
import matplotlib.pyplot as plt
# 독립 변수 및 종속 변수 설정
X = df[["Personalization", "Email_Campaign", "In_App_Notification"]]
y = df["MAU"]
# 모델 학습
model = LinearRegression()
model.fit(X, y)
# 회귀 계수 출력
coefficients = pd.DataFrame({
"Feature": X.columns,
"Coefficient": model.coef_
})
print(coefficients)
# 예측 값 계산
df["Predicted_MAU"] = model.predict(X)
# 성능 평가
mae = mean_absolute_error(df["MAU"], df["Predicted_MAU"])
r2 = r2_score(df["MAU"], df["Predicted_MAU"])
print(f"Mean Absolute Error (MAE): {mae:.2f}")
print(f"R-squared (R²): {r2:.4f}")
# 결과 시각화
plt.figure(figsize=(10, 5))
plt.plot(df["Month"], df["MAU"], label="Actual MAU", marker='o')
plt.plot(df["Month"], df["Predicted_MAU"], label="Predicted MAU", linestyle="dashed", color="red")
plt.xlabel("Month")
plt.ylabel("Monthly Active Users (MAU)")
plt.title("Impact of Growth Marketing Strategies on MAU")
plt.legend()
plt.grid()
plt.show()
- 회귀 계수 (Coefficient):
각 마케팅 전략의 회귀 계수는 해당 전략이 MAU(월별 활성 사용자 수)에 미치는 영향을 수치적으로 나타낸다.- Personalization (개인화 추천 시스템): 회귀 계수는 681.23이다. 이는 개인화 추천 시스템을 도입했을 때 MAU가 평균적으로 681명 증가함을 의미한다.
- Email Campaign (이메일 캠페인): 회귀 계수는 314.61이다. 이메일 캠페인이 실행되면 MAU가 평균적으로 315명 증가한다고 해석할 수 있다.
- In-App Notification (앱 내 알림): 회귀 계수는 8.49로, 상대적으로 작은 영향을 미친다. 이는 앱 내 알림 도입 시 MAU가 약 8명 증가함을 의미한다.
- 모델 성능 평가:
- R² (결정계수): 0.8557로, 이 값은 모델이 실제 MAU 데이터의 변동성을 85.57% 정도 설명하고 있음을 나타낸다. 즉, 모델이 상당히 잘 데이터를 설명하고 있다는 의미.
- MAE (평균 절대 오차): 107.48로, 모델이 예측한 MAU 값과 실제 MAU 값 사이의 평균적인 오차가 107.48명이라는 뜻이다. 이는 예측이 비교적 정확하다는 것을 의미하지만, 여전히 약간의 오차가 있음을 나타낸다.
- 시각화 해석:
- 그래프에서 실제 MAU(실선)와 예측된 MAU(점선)의 변화를 비교하여 모델의 예측 정확도를 시각적으로 확인할 수 있다.
- 두 곡선이 유사한 패턴을 보인다면 모델이 실제 MAU 변화를 잘 반영하고 있다는 의미이다. 반대로 차이가 크다면 모델에 추가적인 변수나 비선형적인 요소를 고려할 필요가 있다.
# 계절성을 고려한 매출 예측 모델 : 더미 변수
3년간(2019~2021년)의 월별 매출 데이터를 분석하여 계절성을 반영한 매출 예측 모델.
특정 월의 매출 패턴은 다음과 같음 :
- 여름(6~8월): 매출 증가
- 겨울(12~2월): 매출 감소
- 봄(3,5월) 및 가을(9,11월) : 중간 수준
이를 기반으로 월별 계절성을 반영한 더미 변수를 생성하여 선형 회귀 모델을 학습하고, 향후 매출 예측에 활용할 수 있도록 한다. → 계절(Season)을 더미 변수로 변환
# 계절성을 고려한 매출 예측 모델 (더미 변수)
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
# 3년간 월별 매출 데이터 (2019~2021)
data = {
'Year': [2019]*12 + [2020]*12 + [2021]*12,
'Month': list(range(1, 13)) * 3,
'Sales': [
100, 120, 150, 200, 250, 300, 320, 310, 280, 230, 150, 110, # 2019년
105, 125, 160, 210, 260, 310, 330, 320, 290, 240, 160, 115, # 2020년
110, 130, 170, 220, 270, 320, 340, 330, 300, 250, 170, 120 # 2021년
]
}
df = pd.DataFrame(data)
# 계절 변수 추가
df['Season'] = df['Month'].apply(lambda x: 'Winter' if x in [12, 1, 2] else
'Spring' if x in [3, 4, 5] else
'Summer' if x in [6, 7, 8] else
'Fall')
# 계절을 더미 변수로 변환 (기준값: Winter)
df = pd.get_dummies(df, columns=['Season'], drop_first=True)
# 독립 변수 (X)와 종속 변수 (Y) 설정
X = df.drop(columns=['Sales', 'Year', 'Month']) # 'Month'는 제거
Y = df['Sales']
# 선형 회귀 모델 생성 및 학습
model = LinearRegression()
model.fit(X, Y)
# 예측
Y_pred = model.predict(X)
# 모델 평가
r2 = r2_score(Y, Y_pred)
print(f"R² Score: {r2:.4f}")
# 회귀 계수 출력
coefficients = pd.DataFrame({'Feature': X.columns, 'Coefficient': model.coef_})
print("\nRegression Coefficients:")
print(coefficients)
# 예측값 데이터프레임에 추가
df['Predicted_Sales'] = Y_pred
# 실제값과 예측값 시각화
plt.figure(figsize=(12, 6))
plt.plot(df.index, df['Sales'], label="Actual Sales", marker="o")
plt.plot(df.index, df['Predicted_Sales'], label="Predicted Sales", linestyle="--", marker="s")
plt.xlabel("Months")
plt.ylabel("Sales")
plt.title("Seasonal Regression with Dummy Variables (Summer ↑, Winter ↓)")
plt.legend()
plt.show()
# 전체 데이터 출력
print("\nData with Predictions:")
print(df.to_string(index=False))
※ 계절을 더미 변수로 변환
df = pd.get_dummies(df, columns=['Season'], drop_first=True)* 설명:
- pd.get_dummies()를 사용해서 계절 변수를 더미 변수(dummy variable)로 변환
- drop_first=True → Winter(겨울)를 기준으로 제거
- 계절이 4개(Winter, Spring, Summer, Fall)라면 3개만 더미 변수로 사용
- 이걸 기준(base category) 라고 하는데, Winter를 기준으로 Spring, Summer, Fall이 매출에 미치는 영향만 분석하는 방식
- 변환 후 데이터 예시
| Year | Month | Sales | Season_Spring | Season_Summer | Season_Fall |
| 2019 | 1 | 100 | 0 | 0 | 0 |
| 2019 | 2 | 120 | 0 | 0 | 0 |
| 2019 | 3 | 150 | 1 | 0 | 0 |
| 2019 | 6 | 300 | 0 | 1 | 0 |
| 2019 | 10 | 230 | 0 | 0 | 1 |
Winter는 기준값이라 표시되지 않음 (Season_Winter 없음)
Season_Spring = 1이면 봄(Spring), Season_Summer = 1이면 여름(Summer), Season_Fall = 1이면 가을(Fall)
※ 더미 변수(dummy variable)
- 범주형 데이터를 숫자로 변환할 때 사용
- 특정 카테고리에 속하면 1, 아니면 0
- 다중공선성 문제를 방지하기 위해 drop_first=True 설정
계절성을 고려한 회귀분석에서 더미변수를 사용하는 이유
계절성을 고려한 회귀분석에서는 월(month)이나 분기(quarter)와 같은 범주형 변수(categorical variable)를 어떻게 모델에 반영할지 고민해야 한다. 이때, 더미 변수(dummy variable) 를 사용하면 계절성을 효과적으로 반영할 수 있다.
더미 변수가 필요한 이유
▶ 범주형 변수를 수치형 변수로 변환해야 하기 때문
- 선형 회귀 모델은 수치형 변수(숫자) 만 사용할 수 있다.
- 하지만 월(Month) 같은 변수는 숫자처럼 보이지만 실제로는 범주형 데이터이다.
- 예: 1월(1), 2월(2), 3월(3) ... 12월(12)
- 숫자로 해석하면 순서가 있는 것처럼 보이지만, 실제로는 연속적인 의미가 없음.
- 이런 데이터를 그대로 넣으면 잘못된 분석 결과가 나올 수 있음.
해결 방법:
- 각 월을 독립적인 변수로 변환 → 더미 변수 생성.
- Month_1, Month_2, ..., Month_12 같은 이진 변수(0 또는 1)로 표현
인공신경망의 기본 구조 & 역전파와 딥러닝 모델 학습 설명
# 인공신경망(Artificial Neural Network, ANN)의 기본 구조
인공신경망(ANN)은 인간의 신경망을 모방하여 만들어진 모델로, 입력층, 은닉층, 출력층으로 구성
| 구조 | 설명 |
| 입력층(Input Layer) | 입력 데이터를 받아들이는 층 |
| 은닉층(Hidden Layer) | 여러 개의 뉴런(Neuron)으로 구성되어 입력을 변환하는 층 |
| 출력층(Output Layer) | 최종 예측 값을 출력하는 층 |
☆ 각각의 은닉층(hidden layer)은 Dense 레이어로 구성된다. Dense는 입력과 출력이 모두 연결되는 Fully Connected Layer이다.
☆ 출력 노드가 여러 개 있으면 분류이다.
☆ 출력 노드가 하나이면 회귀이다.
☆ 소프트맥스 함수를 쓰면 무조건 분류!
각 뉴런은 활성화 함수(Activation Function)를 통해 비선형성을 추가하여 학습 능력을 강화한다.
※ 각각의 층은 활성화 함수를 포함.
※ 대표적 활성화 함수
1) 시그모이드 (Sigmoid)
2) 하이퍼볼릭 탄젠트 (Hyperbolic Tangent)
3) 렐루 (ReLU)
4) 소프트맥스 (Softmax)
# 역전파(Backpropagation) & 딥러닝 학습
- 역전파(Backpropagation)는 신경망의 가중치를 업데이트하는 알고리즘으로, 오차를 최소화하기 위해 가중치를 조정하는 과정이다.
역전파 과정
※ 기울기(가중치)만 바꿈.
1. 순전파(Forward Propagation) - 전방향 학습
- 입력 데이터를 각 층을 거쳐 출력층까지 전달
- 출력값을 계산하여 손실 함수(Loss Function)를 통해 오차를 계산
2. 손실 계산(Loss Calculation)
- 예측값과 실제값의 차이를 계산하여 오차를 측정
- 예: 평균제곱오차(Mean Squared Error, MSE) - 이걸로 손실 계산
3. 역전파(Backward Propagation) - 다시 w바꾸기
- 손실을 기반으로 각 가중치에 대한 기울기(Gradient)를 계산
- 체인룰(Chain Rule)을 사용하여 미분을 수행하여 기울기(Gradient) 계산
4. 가중치 업데이트(Weight Update)
- 경사 하강법(Gradient Descent)을 사용하여 가중치를 업데이트
- 가중치 업데이트:

# 인공신경망 학습의 수식





- 인공신경망 학습 코드
import numpy as np
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
# 데이터 생성 (XOR 문제를 확장한 예제)
np.random.seed(42)
X = np.random.rand(1000, 2) * 2 - 1 # [-1, 1] 범위의 랜덤 데이터
y = (X[:, 0] * X[:, 1] > 0).astype(int) # XOR 패턴
# 데이터 분할
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 데이터 정규화
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)
# 인공신경망 모델 정의
model = Sequential([
Dense(8, activation='relu', input_shape=(2,)), # 은닉층 1
Dense(8, activation='relu'), # 은닉층 2
Dense(1, activation='sigmoid') # 출력층 (이진 분류)
])
# 모델 컴파일 (손실 함수 & 최적화 알고리즘 정의)
model.compile(optimizer='adam', loss='binary_crossentropy', metrics=['accuracy'])
# 모델 학습
history = model.fit(X_train, y_train, epochs=100, batch_size=16, validation_data=(X_test, y_test))
# 모델 평가
loss, accuracy = model.evaluate(X_test, y_test)
print(f"Test Accuracy: {accuracy:.4f}")
# 예측값 확인
predictions = (model.predict(X_test) > 0.5).astype(int)
print("\nPredictions:")
print(predictions[:10])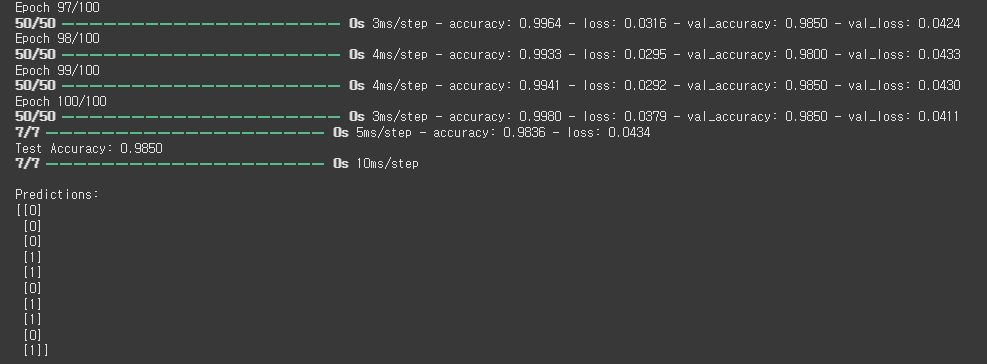
- 모델 구조
- 입력층: 2개의 입력 뉴런
- 은닉층: 8개 뉴런 × 2개층 (ReLU 활성화 함수 사용)
- 출력층: 1개 뉴런 (Sigmoid 활성화 함수 사용)
- 손실 함수 & 최적화 기법
- 이진 분류 문제이므로 binary_crossentropy 사용
- Adam 최적화(adam): 가중치 업데이트 자동 조정
- 모델 학습 과정
- 100 Epoch 동안 학습 수행
- 학습 데이터(train)와 검증 데이터(test) 성능 비교
- 예측 결과
- 학습된 모델로 테스트 데이터에 대한 예측 수행
※ batch size - 1번에 데이터를 읽는 개수.
※ # 모델 컴파일 부분, # 모델학습 부분 주의해서 보기.
- 역전파 학습이 진행되는 과정을 그래프로 표현
→ 그래프를 보고 학습량 조절 위해
- 손실 함수 값(예: binary_crossentropy)이 학습 과정에서 어떻게 감소하는지를 시각화.
- matplotlib을 사용하여 학습 과정에서의 손실 값(loss) 및 정확도(accuracy) 변화를 그래프로 표현.
# 역전파 학습이 진행되는 과정을 그래프로 표현
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
# 데이터 생성 (XOR 패턴 확장)
np.random.seed(42)
X = np.random.rand(1000, 2) * 2 - 1 # [-1, 1] 범위의 랜덤 데이터
y = (X[:, 0] * X[:, 1] > 0).astype(int) # XOR 패턴
# 데이터 분할
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 데이터 정규화
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)
# 인공신경망 모델 정의
model = Sequential([
Dense(8, activation='relu', input_shape=(2,)), # 은닉층 1
Dense(8, activation='relu'), # 은닉층 2
Dense(1, activation='sigmoid') # 출력층 (이진 분류)
])
# 모델 컴파일 (손실 함수 & 최적화 알고리즘 정의)
model.compile(optimizer='adam', loss='binary_crossentropy', metrics=['accuracy'])
# 모델 학습 (손실 및 정확도 기록)
history = model.fit(X_train, y_train, epochs=100, batch_size=16, validation_data=(X_test, y_test))
# 학습 과정 시각화
fig, ax1 = plt.subplots(figsize=(10, 5))
# 손실(loss) 그래프
ax1.plot(history.history['loss'], label='Training Loss', color='blue')
ax1.plot(history.history['val_loss'], label='Validation Loss', color='red', linestyle="--")
ax1.set_xlabel('Epochs')
ax1.set_ylabel('Loss')
ax1.set_title('Loss & Accuracy During Training')
ax1.legend(loc='upper right')
# 정확도(accuracy) 그래프 (y축 공유)
ax2 = ax1.twinx()
ax2.plot(history.history['accuracy'], label='Training Accuracy', color='green')
ax2.plot(history.history['val_accuracy'], label='Validation Accuracy', color='orange', linestyle="--")
ax2.set_ylabel('Accuracy')
ax2.legend(loc='lower right')
plt.show()
- 파랑곡선 - 0.75정도의 손실이 있었는데 epoch 100번하면서 거의 0에 근접함.
- 초록곡선 - 반복했을때 정확도는 100퍼센트에 가까워진다.
- 그래프를 그려보면 얼마나 epoch 해야하는지 알 수 있다. (학습량 조절)
- 데이터 생성
- 랜덤으로 데이터를 생성하고 XOR 패턴을 따른 y 값을 설정.
- StandardScaler를 사용하여 데이터 정규화.
- 신경망 모델 구성
- 은닉층 2개 (ReLU 활성화 함수 사용)
- 출력층 1개 (Sigmoid 활성화 함수 사용)
- adam 옵티마이저와 binary_crossentropy 손실 함수 사용
- 학습 및 손실 기록
- model.fit()을 수행하여 loss와 accuracy 값을 저장
- 그래프 시각화
- 파란색(blue) 선: 훈련 데이터 손실(Training Loss)
- 빨간색(red) 점선: 검증 데이터 손실(Validation Loss)
- 초록색(green) 선: 훈련 정확도(Training Accuracy)
- 주황색(orange) 점선: 검증 정확도(Validation Accuracy)
- twinx()를 사용하여 손실과 정확도를 같은 그래프에 표시
# 개인화된 추천 시스템 도입, 이메일 캠페인, 앱 내 알림 등이 월별 활성 사용자 수(MAU) 에 어떤 영향을 미쳤는지 분석 - Deep Learning으로 구현
- 라이브러리 우선 설치
!pip install --upgrade keras tensorflow
- 코드
import numpy as np
import pandas as pd
import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Dropout, BatchNormalization, Input
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_absolute_error, r2_score
import matplotlib.pyplot as plt
# 데이터 생성
np.random.seed(42)
months = np.arange(1, 13) # 12개월 데이터
base_users = 10000
# 마케팅 전략 실행 여부
personalization = np.array([0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1])
email_campaign = np.array([0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1])
in_app_notification = np.array([0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1])
# 월별 MAU 계산
mau = base_users * (1 + personalization * 0.05 + email_campaign * 0.03 + in_app_notification * 0.02)
mau += np.random.normal(0, 200, size=len(months)) # 노이즈 추가
# 데이터프레임 생성
df = pd.DataFrame({
"Month": months,
"Personalization": personalization,
"Email_Campaign": email_campaign,
"In_App_Notification": in_app_notification,
"MAU": mau
})
# 독립 변수 및 종속 변수 설정
X = df[["Personalization", "Email_Campaign", "In_App_Notification"]]
y = df["MAU"]
# 데이터 정규화
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
# 모델 생성 (input_shape을 Input() 레이어로 변경)
model = Sequential()
model.add(Input(shape=(X_scaled.shape[1],)))
model.add(Dense(64, activation=tf.keras.activations.relu))
model.add(BatchNormalization())
model.add(Dropout(0.2))
model.add(Dense(32, activation=tf.keras.activations.relu))
model.add(BatchNormalization())
model.add(Dropout(0.2))
model.add(Dense(16, activation=tf.keras.activations.relu))
model.add(Dense(1)) # 출력층 (MAU 예측)
# 모델 컴파일
model.compile(optimizer='adam', loss='mse', metrics=['mae'])
# 모델 학습
history = model.fit(X_scaled, y, epochs=2000, batch_size=4, validation_split=0.2, verbose=0)
# 예측 값 계산
y_pred = model.predict(X_scaled).flatten()
# 성능 평가
mae = mean_absolute_error(y, y_pred)
r2 = r2_score(y, y_pred)
print(f"Mean Absolute Error (MAE): {mae:.2f}")
print(f"R-squared (R²): {r2:.4f}")
# 시각화
plt.figure(figsize=(10, 5))
plt.plot(df["Month"], df["MAU"], label="Actual MAU", marker='o')
plt.plot(df["Month"], y_pred, label="Predicted MAU", linestyle="dashed", color="red")
plt.xlabel("Month")
plt.ylabel("Monthly Active Users (MAU)")
plt.title("Impact of Growth Marketing Strategies on MAU (DNN Model)")
plt.legend()
plt.grid()
plt.show()
※ 위 코드로 epoch를 2000번 했을때와 200번 했을때의 비교
- 에폭수를 맞춰서 최적의 epoch값을 찾고 싶었으나 상당히...시간이 오래걸려서...패스
우선 데이터 자체가 많지 않아서 모델 성능이 떨어져서 그런가 R-squared값과 MAE값이 엉망이다.
→ 딥러닝은 아주 많은 양의 데이터가 있을시 적합한 방법이다.


epoch수 = w를 업데이트하는 과정. 반복학습이 손실함수에 주는 영향 확인.
epoch이 반복될때마다 w는 손실함수가 0이 되는 방향으로 업데이트.
# 계절성을 고려한 매출 예측 모델(DNN)
3년간(2019~2021년)의 월별 매출 데이터를 분석하여 계절성을 반영한 매출 예측 모델.
특정 월의 매출 패턴은 다음과 같음 :
- 여름(6~8월): 매출 증가
- 겨울(12~2월): 매출 감소
- 봄(3,5월) 및 가을(9,11월) : 중간 수준
- DNN Learning (모델 만들어서 저장)
# 모델 만들어서 저장하는 코드
import numpy as np
import pandas as pd
import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Dropout, BatchNormalization
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
import joblib
# 데이터 생성 (3년간 월별 매출)
data = {
'Year': [2019]*12 + [2020]*12 + [2021]*12,
'Month': list(range(1, 13)) * 3,
'Sales': [
100, 120, 150, 200, 250, 300, 320, 310, 280, 230, 150, 110,
105, 125, 160, 210, 260, 310, 330, 320, 290, 240, 160, 115,
110, 130, 170, 220, 270, 320, 340, 330, 300, 250, 170, 120
]
}
df = pd.DataFrame(data)
# 계절 변수 추가 (Winter 포함)
df['Season'] = df['Month'].apply(lambda x: 'Winter' if x in [12, 1, 2] else
'Spring' if x in [3, 4, 5] else
'Summer' if x in [6, 7, 8] else
'Fall')
# 계절을 더미 변수로 변환 (Winter 포함, drop_first=False 유지)
df = pd.get_dummies(df, columns=['Season'], drop_first=False)
# 독립 변수(X)와 종속 변수(Y) 설정
X = df.drop(columns=['Sales', 'Year', 'Month'])
Y = df['Sales']
# 데이터 정규화
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
# 데이터 분할 (Train/Test)
X_train, X_test, Y_train, Y_test = train_test_split(X_scaled, Y, test_size=0.2, random_state=42)
# 모델 생성
model = Sequential([
Dense(64, activation='relu', input_shape=(X_train.shape[1],)),
BatchNormalization(),
Dropout(0.2),
Dense(32, activation='relu'),
BatchNormalization(),
Dropout(0.2),
Dense(16, activation='relu'),
Dense(1)
])
# 모델 컴파일 (손실 함수를 문자열 대신 객체로 지정)
model.compile(optimizer='adam', loss=tf.keras.losses.MeanSquaredError(), metrics=['mae'])
# Early Stopping 설정 (과적합 방지)
early_stopping = tf.keras.callbacks.EarlyStopping(
patience=10, restore_best_weights=True
)
# 모델 학습
history = model.fit(X_train, Y_train, epochs=200, batch_size=4,
validation_data=(X_test, Y_test), callbacks=[early_stopping], verbose=0)
# 모델 평가
loss, mae = model.evaluate(X_test, Y_test)
print(f"Test Mean Absolute Error (MAE): {mae:.2f}")
# 모델 저장
model.save("sales_prediction_model.h5")
print("모델이 'sales_prediction_model.h5'로 저장되었습니다.")
# 정규화 객체 저장
joblib.dump(scaler, "scaler.pkl")
print("입력 데이터 정규화를 위한 scaler.pkl 파일이 저장되었습니다.")
# 저장된 feature 정보 저장 (나중에 같은 feature 순서를 유지하기 위해)
joblib.dump(X.columns.tolist(), "feature_names.pkl")
print("입력 데이터의 feature 정보가 feature_names.pkl 파일로 저장되었습니다.")
- Model test (저장된 모델을 로딩해서 처리)
# 저장된 모델을 불러와서 예측 테스트
import numpy as np
import pandas as pd
import tensorflow as tf
import joblib
# 저장된 모델 로드
loaded_model = tf.keras.models.load_model("sales_prediction_model.h5")
loaded_model.compile(optimizer='adam', loss=tf.keras.losses.MeanSquaredError(), metrics=['mae'])
print("저장된 모델이 로드되었습니다.")
# 저장된 정규화 객체 및 feature 정보 로드
scaler = joblib.load("scaler.pkl")
feature_names = joblib.load("feature_names.pkl")
# 새로운 입력값 생성 (훈련 데이터와 동일한 feature 순서 유지)
new_data = pd.DataFrame(columns=feature_names, data=[[0, 1, 0, 0]]) # 봄(Season_Spring=1)
print("새로운 입력값:")
print(new_data)
# 입력값 정규화
new_data_scaled = scaler.transform(new_data)
# 예측 수행
predicted_sales = loaded_model.predict(new_data_scaled).flatten()
print(f"예측된 매출: {predicted_sales[0]:.2f}")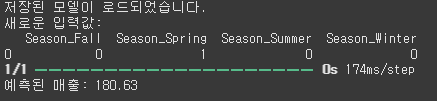
※ dropout → 과적합을 방지하고 모델의 일반화 능력을 높이기 위해 사용. 일부 뉴런을 훈련 중에 임의로 꺼버리는 기법. 이를 통해 모델이 특정 뉴런에 의존하지 않고 더 일반화될 수 있도록 도와줌. w(가중치)에 0을 곱하는 방식.
'데이터 분석 part' 카테고리의 다른 글
| LSTM 이해와 마케팅 데이터를 활용한 실습, LSTM 모델 성능평가 (0) | 2025.03.18 |
|---|---|
| 차원축소, 계층적 군집 분석, 시계열데이터 예측 (회귀분석, 이동평균(MA), 지수 가중 이동 평균 (EMA)) / 마케팅 보고서 작성 연습 (1) | 2025.03.14 |
| 인공신경망(ANN), 다층신경망(MLP), 심층신경망(DNN) / ( 결정트리, 랜덤포레스트, K-평균군집화 복습 ) (0) | 2025.03.13 |
| k-NN 알고리즘, 서포트 벡터 머신(SVM), flask 웹실습 (2) | 2025.03.13 |
| 모델 성능 평가와 다중 분류 / 결정 트리의 기본 개념 / 랜덤 포레스트 개념과 구현 (0) | 2025.03.11 |