< 데이터 전처리 >
- 데이터를 머신러닝 모델에 적합한 형태로 변환
1) 데이터 정리 및 탐색
- 데이터 로드: pandas, NumPy 등을 활용하여 데이터를 불러옴
- 기초 통계 확인: df.describe(), df.info() 등을 이용하여 데이터 타입과 분포 확인
- 데이터 시각화: matplotlib, seaborn을 사용해 변수 간 관계 파악
2) 결측값(Missing Values) 처리
(1) 결측값 확인
import pandas as pd
df.isnull().sum() # 결측값 개수 확인
(2) 결측값 처리 방법
# 삭제(Dropping): 결측값이 적은 경우 해당 행 또는 열 제거
df.dropna(inplace=True)
# 대체(Imputation): 평균, 중앙값, 최빈값 또는 예측값으로 결측값을 채움
df.fillna(df.mean(), inplace=True) # 평균값으로 대체
df.fillna(df.median(), inplace=True) # 중앙값으로 대체
df.fillna(df.mode().iloc[0], inplace=True) # 최빈값으로 대체
# 예측 모델 활용: 머신러닝 모델을 이용해 결측값을 예측하고 보완
3) 이상치(Outliers) 처리
(1) 이상치 탐색
# 박스플롯(Box Plot) 활용
import seaborn as sns
sns.boxplot(x=df['feature_column'])
# Z-Score 활용
from scipy import stats
z_scores = stats.zscore(df['feature_column'])
df = df[(z_scores < 3)] # Z-score가 3 이상이면 이상치로 간주하여 제거
# IQR(Interquartile Range, 사분위 범위) 활용
Q1 = df['feature_column'].quantile(0.25)
Q3 = df['feature_column'].quantile(0.75)
IQR = Q3 - Q1
df = df[(df['feature_column'] >= Q1 - 1.5 * IQR) & (df['feature_column'] <= Q3 + 1.5 * IQR)]
(2) 이상치 처리 방법
- 제거(Removal): 이상치를 제거하는 방식
- 대체(Replacement): 중앙값 또는 평균값으로 변경
- 변환(Transformation): 로그 변환, 제곱근 변환 등 사용
4) 데이터 정규화 및 스케일링
특징 값(Feature Value)의 크기가 다를 경우 모델 성능에 영향을 미칠 수 있으므로 스케일링을 수행해야 한다.
(1) 정규화(Normalization)
- 모든 값을 0~1 범위로 변환
- MinMaxScaler 사용
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler()
df[['feature1', 'feature2']] = scaler.fit_transform(df[['feature1', 'feature2']])
(2) 표준화(Standardization)
- 평균이 0, 표준편차가 1이 되도록 변환
- StandardScaler 사용
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
df[['feature1', 'feature2']] = scaler.fit_transform(df[['feature1', 'feature2']])< 특징 엔지니어링(Feature Engineering) >
- 모델이 학습할 수 있도록 적절한 특징을 생성하거나 변환하는 과정.
1) 새로운 특징 생성
새로운 변수(Feature)를 추가하여 모델의 성능 향상
(1) 기존 변수 조합
- 예) 키와 몸무게를 이용해 BMI(체질량지수) 생성
df['BMI'] = df['Weight'] / (df['Height']**2)
(2) 날짜 정보 변환
- 날짜 데이터를 요일, 월, 연도 등으로 변환
df['date'] = pd.to_datetime(df['date'])
df['year'] = df['date'].dt.year
df['month'] = df['date'].dt.month
df['day'] = df['date'].dt.day
df['weekday'] = df['date'].dt.weekday # 0: 월요일, 6: 일요일
(3) 텍스트 데이터 변환
- 단어 빈도수, TF-IDF 벡터화 등을 활용해 숫자로 변환
※ TF-IDF 벡터화 - 해당 단어의 빈도수를 가지고 처리함
from sklearn.feature_extraction.text import TfidfVectorizer
vectorizer = TfidfVectorizer()
tfidf_matrix = vectorizer.fit_transform(df['text_column'])
2) 특징 선택(Feature Selection)
- 변수들 중에서 모델 성능을 높이는 중요한 변수만 선택하는 과정
(1) 상관계수(Correlation) 활용
- 높은 상관관계를 가진 변수만 선택
import seaborn as sns
import matplotlib.pyplot as plt
corr_matrix = df.corr()
sns.heatmap(corr_matrix, annot=True, cmap="coolwarm")
(2) 중요도 기반 선택
- 랜덤 포레스트 모델을 사용해 변수 중요도를 확인
※ 랜덤 포레스트 - 여러 개의 decision tree를 이어 붙인 것
from sklearn.ensemble import RandomForestClassifier
model = RandomForestClassifier()
model.fit(X_train, y_train)
feature_importances = pd.Series(model.feature_importances_, index=X_train.columns)
feature_importances.sort_values(ascending=False).plot(kind='bar')
3) 특징 변환(Feature Transformation)
- 특징을 변환하여 데이터의 분포를 변경하거나 차원을 축소
(1) 로그 변환(Log Transformation)
- 분포가 오른쪽으로 치우쳐 있는 경우 로그 변환을 통해 정규 분포에 가깝게 만듦
df['feature'] = np.log1p(df['feature'])
(2) 차원 축소(Dimensionality Reduction)
- PCA(주성분 분석)을 이용해 특징 차원을 줄임
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X)
회귀분석의 개념
주요 구성요소
- 종속 변수 (Dependent Variable, Y) : 분석의 목표가 되는 변수, 라벨
- 독립 변수 (Independent Variable, X) : 종속 변수에 영향을 주는 변수
- 오차항 (Error Term, ε, 잔차) : 모델이 설명하지 못하는 부분, 관측된 값과 예측된 값 사이의 차이, 측정오차나 누락된 변수 등
회귀모델의 형태
주어진 데이터에 가장 적합한 함수를 찾는다. 함수는 선형(linear) 또는 비선형(nonlinear) 형태를 가질 수 있으며, 대표적인 방법으로 최소제곱법(OLS, Ordinary Least Squares)을 사용하여 모델의 파라미터를 추정한다.
< 단순 선형 회귀 분석 >
하나의 독립 변수와 하나의 종속 변수 사이의 선형 관계를 모델링
수식

최소제곱법 (OLS)
최소제곱법을 통해 B0와 B1를 추정. 각 관측치에서 예측값과 실제값 사이의 잔차(residual)의 제곱합을 최소화하는 파라미터를 찾는 방법이다.
- 잔차 분석: 잔차를 분석하면 모델이 데이터의 변동성을 얼마나 잘 설명하는지, 그리고 이상치나 패턴이 존재하는지 확인할 수 있음.
회귀분석의 기본 가정
1) 선형성 (Linearity)
독립 변수와 종속 변수 간의 관계가 선형이라는 가정.
데이터가 선형적이지 않을 경우 비선형 변환이나 다른 모델링 기법이 필요할 수 있음.
2) 독립성 (Independence)
각 관측치가 서로 독립적이어야 한다.
시간 순서가 있는 데이터(예: 시계열 데이터)의 경우 자기상관 문제가 발생할 수 있으며, 이를 확인하고 보정할 필요가 있음.
3) 등분산성 (Homoscedasticity)
모든 수준의 독립 변수에서 오차의 분산이 동일하다는 가정.
만약 오차의 분산이 일정하지 않다면(이분산성, 실제값과 추정값의 차이가 많다), 모델의 추정치가 왜곡될 수 있음.
4) 정규성 (Normality)
오차항이 정규분포를 따른다는 가정.
이는 주로 추정치의 신뢰구간 및 가설 검정에서 중요한 역할을 하며, 정규성 검정을 통해 확인할 수 있음.
모델 적합도 평가 및 검정
단순 회귀 분석을 통해 얻은 모델의 유의성과 적합도를 평가.
1) 결정계수 (R²) - 가장 많이 씀
- R² 값: 종속 변수의 변동 중에서 모델이 설명하는 비율. 0과 1 사이의 값을 가지며, 1에 가까울수록 모델의 설명력이 좋음.


2) t-검정 및 p-값
- t-검정: 각 회귀계수가 통계적으로 유의한지를 검정.
- p-값: 기울기나 절편이 0이라는 귀무가설을 기각할 수 있는지 판단. 일반적으로 p-값이 0.05 미만이면 유의하다고 봄.
3) F-검정
- 전체 모델의 유의성을 검정하는 방법으로, 독립 변수가 종속 변수의 변동을 설명하는 데 유의한지 평가.
한계와 주의점
- 상관관계와 인과관계: 회귀분석은 변수 간 상관관계를 분석하지만, 인과관계를 확정하지는 않는다.
- 가정 위배: 선형성, 독립성, 등분산성, 정규성 등의 가정이 위배되면 모델의 추정치와 해석에 문제가 발생할 수 있음.
- 외생 변수: 중요한 독립 변수가 누락되면, 결과가 왜곡될 수 있음.
- 이상치의 영향: 이상치는 회귀계수 추정에 큰 영향을 미칠 수 있으므로, 데이터 전처리와 이상치 처리가 필요.
- 광고비(독립 변수)와 전환수(종속 변수) 간의 관계를 단순 회귀 분석하는 예시코드
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
# 1. 가상의 데이터 준비
data = {
'ad_spend': [1000, 2000, 3000, 4000, 5000, 6000, 7000, 8000, 9000, 10000],
'conversions': [120, 150, 180, 210, 240, 265, 290, 320, 345, 370]
}
df = pd.DataFrame(data)
# 2. 독립 변수(X)와 종속 변수(y) 설정
X = df[['ad_spend']]
y = df['conversions']
# 3. 단순 회귀 모델 생성 및 학습
model = LinearRegression()
model.fit(X, y)
# 4. 모델 파라미터 및 결정계수(R²) 출력
intercept = model.intercept_
slope = model.coef_[0]
r2 = r2_score(y, model.predict(X))
print("회귀식: 전환수 = {:.2f} + {:.5f} * 광고비".format(intercept, slope))
print("결정계수 (R²): {:.4f}".format(r2))
# 5. 예측 및 시각화
df['predicted_conversions'] = model.predict(X)
plt.scatter(df['ad_spend'], df['conversions'], color='blue', label='실제 전환수')
plt.plot(df['ad_spend'], df['predicted_conversions'], color='red', label='회귀 직선')
plt.title('광고비 대비 전환수 분석')
plt.xlabel('광고비 ($)')
plt.ylabel('전환수')
plt.legend()
plt.show()
< 다중 선형 회귀 분석>
- 하나의 종속 변수(타겟 변수)를 여러 개의 독립 변수(설명 변수)를 사용하여 예측

- 다중 선형 회귀 모델을 학습하는 과정에서는 최소제곱법(OLS, Ordinary Least Squares) 을 사용하여 회귀 계수들을 최적화한다.
모델 평가 지표
다중 선형 회귀 모델의 성능을 평가하기 위해 다음과 같은 주요 평가 지표를 사용한다.
(1) 결정 계수 (R-squared)
- 모델이 실제 데이터를 얼마나 잘 설명하는지를 나타내는 지표
- 값이 1에 가까울수록 모델이 데이터를 잘 설명하는 것이며, 0에 가까울수록 설명력이 낮다.


(2) 평균 제곱 오차 (MSE, Mean Squared Error)
- 예측값과 실제값 간의 오차를 제곱하여 평균을 구한 값.
- 값이 작을수록 모델의 예측 성능이 좋음을 의미한다.

(3) 평균 절대 오차 (MAE, Mean Absolute Error)
- 예측값과 실제값 간의 절대 차이의 평균을 구한 값.
- MSE보다 이상치(outlier)에 덜 민감한 지표.
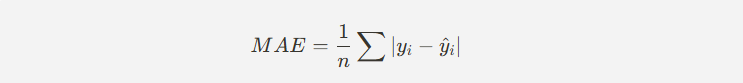
(4) 평균 절대 백분율 오차 (MAPE, Mean Absolute Percentage Error)
- 예측값과 실제값 간의 차이를 백분율로 변환하여 평균을 구한 값.
- 상대적인 오차를 측정할 때 유용.

다중 선형 회귀 모델의 가정
1) 선형성 (Linearity)
- 독립 변수(X)와 종속 변수(Y) 간의 관계가 선형이어야 한다.
- 즉, 독립 변수가 증가하거나 감소할 때 종속 변수도 일정한 비율로 증가하거나 감소해야 한다.
- 선형성이 깨지면 모델이 올바르게 예측하지 못할 수 있다.
2) 독립성 (Independence)
- 독립 변수들끼리는 서로 상관관계가 없어야 한다.
- 독립 변수 간에 다중 공선성(Multicollinearity)이 있으면 회귀 모델의 신뢰성이 떨어진다.
- 다중 공선성이 존재하면 특정 변수의 중요도를 해석하기 어려워진다.
3) 등분산성 (Homoscedasticity)
- 독립 변수의 값이 변화하더라도 오차(Residual)의 분산이 일정해야 한다.
- 만약 등분산성이 깨지면 모델의 예측 성능이 특정 구간에서만 좋고, 다른 구간에서는 나쁠 수 있다.
- 이를 해결하기 위해 로그 변환, 정규화 등의 기법을 사용할 수 있다.
4) 정규성 (Normality of Errors)
- 회귀 모델의 오차(Residuals)는 정규 분포를 따라야 한다.
- 오차가 정규성을 가지면 회귀 계수의 신뢰 구간을 정확하게 계산할 수 있고, 모델의 예측이 안정적이다.
- 정규성이 깨지면 t-검정이나 F-검정과 같은 통계적 검정이 잘못된 결론을 내릴 가능성이 높아진다.
다중 선형 회귀 모델이 올바르게 작동하려면 위의 네 가지 가정을 충족해야 한다. 현실에서는 데이터가 항상 이상적인 가정을 만족하지 않으므로, 데이터 전처리, 변수 변환, 다중 공선성 제거, 정규화 기법 등을 활용하여 모델 성능을 향상시킬 필요가 있다. 위 가정을 만족하지 않을 경우, 다중 선형 회귀 모델이 적절하지 않을 수 있으며, 변환 기법이나 다른 모델을 고려해야 한다.
선형성(Linearity) 검토
- 예제: 공부 시간과 시험 점수의 관계를 선형 회귀로 분석
- 해결 방법: 다항 변환 (Polynomial Features)
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
# 데이터 생성 (선형 관계가 아님)
X = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10]).reshape(-1, 1)
y = np.array([2, 5, 9, 15, 22, 31, 42, 55, 70, 88]) # 비선형 관계
# 선형 회귀 모델
linear_reg = LinearRegression()
linear_reg.fit(X, y)
y_pred = linear_reg.predict(X)
# 다항 회귀 적용 (2차 변환)
poly = PolynomialFeatures(degree=2)
X_poly = poly.fit_transform(X)
poly_reg = LinearRegression()
poly_reg.fit(X_poly, y)
y_poly_pred = poly_reg.predict(X_poly)
# 시각화
plt.scatter(X, y, color="blue", label="실제 데이터")
plt.plot(X, y_pred, color="red", linestyle="dashed", label="선형 회귀 예측")
plt.plot(X, y_poly_pred, color="green", label="다항 회귀 예측")
plt.xlabel("공부 시간")
plt.ylabel("시험 점수")
plt.legend()
plt.title("선형성 검토: 선형 vs 다항 회귀")
plt.show()선형성이 깨진 경우 다항 회귀(Polynomial Regression) 등을 적용하여 관계를 보정할 수 있다.
독립성(Independence) 검토
- 예제: 집값 예측에서 다중 공선성 검토
- 해결 방법: VIF (Variance Inflation Factor) 사용하여 공선성 확인 및 제거
import pandas as pd
import statsmodels.api as sm
from statsmodels.stats.outliers_influence import variance_inflation_factor
# 예제 데이터 생성
data = {
"house_size": [50, 60, 70, 80, 90, 100, 110, 120, 130, 140], # 집 크기
"num_rooms": [3, 3, 4, 4, 5, 5, 6, 6, 7, 7], # 방 개수 (집 크기와 강한 상관)
"price": [200, 250, 300, 350, 400, 450, 500, 550, 600, 650] # 집값
}
df = pd.DataFrame(data)
# 다중 공선성 검토
X = df[["house_size", "num_rooms"]]
X = sm.add_constant(X) # 상수 추가
vif_data = pd.DataFrame()
vif_data["Feature"] = X.columns
vif_data["VIF"] = [variance_inflation_factor(X.values, i) for i in range(X.shape[1])]
print(vif_data)VIF 값이 10 이상이면 다중 공선성이 존재하는 것으로 간주하고 해당 변수를 제거하거나 차원을 축소해야 한다.
등분산성(Homoscedasticity) 검토
- 예제: 소득과 소비 데이터에서 잔차 분석
- 해결 방법: 로그 변환, 가중 회귀 적용
import seaborn as sns
from sklearn.linear_model import LinearRegression
# 데이터 생성 (소득에 따라 소비 변화가 일정하지 않음)
income = np.array([20, 25, 30, 35, 40, 50, 60, 80, 100, 150]).reshape(-1, 1)
spending = np.array([5, 7, 10, 12, 15, 22, 30, 45, 60, 100]) # 고소득층에서 변화가 큼
# 회귀 분석
model = LinearRegression()
model.fit(income, spending)
predictions = model.predict(income)
# 잔차 분석
residuals = spending - predictions
# 시각화
plt.scatter(income, residuals, color="blue")
plt.axhline(y=0, color="red", linestyle="dashed")
plt.xlabel("소득")
plt.ylabel("잔차 (Residuals)")
plt.title("등분산성 검토: 잔차 분석")
plt.show()잔차의 분산이 일정하지 않다면 로그 변환 또는 가중 회귀(Weighted Regression) 를 적용하여 해결할 수 있다.
정규성(Normality of Errors) 검토
- 예제: 시험 점수 예측에서 오차(Residuals) 정규성 검토
- 해결 방법: Q-Q Plot, 정규성 검정(Shapiro-Wilk Test)
from scipy import stats
import statsmodels.api as sm
# 데이터 생성 (정규성을 따르지 않는 예제)
np.random.seed(42)
X = np.random.normal(50, 10, 100).reshape(-1, 1)
y = 3 * X.squeeze() + np.random.exponential(10, 100) # 지수 분포 노이즈 추가
# 회귀 모델
model = LinearRegression()
model.fit(X, y)
predictions = model.predict(X)
# 잔차 계산
residuals = y - predictions
# Q-Q Plot (잔차의 정규성 검토)
sm.qqplot(residuals, line='45')
plt.title("Q-Q Plot을 통한 정규성 검토")
plt.show()
# Shapiro-Wilk Test (정규성 검정)
shapiro_test = stats.shapiro(residuals)
print(f"Shapiro-Wilk Test p-value: {shapiro_test.pvalue}")Q-Q Plot에서 점들이 직선을 벗어나면 정규성이 깨진 것.
Shapiro-Wilk Test의 p-value < 0.05이면 정규성이 깨진 것으로 판단.
이를 해결하기 위해 로그 변환(Log Transformation), Box-Cox 변환 등을 적용할 수 있다.
☆☆ ☆☆ ☆☆
| 가정 | 설명 | 해결 방법 |
| 선형성 (Linearity) | 독립 변수와 종속 변수 간 선형 관계 필요 | 다항 회귀(Polynomial Regression) 적용 |
| 독립성 (Independence) | 독립 변수 간 다중 공선성 제거 필요 | VIF 값 확인 후 변수 제거 |
| 등분산성 (Homoscedasticity) | 오차의 분산이 일정해야 함 | 로그 변환, 가중 회귀 적용 |
| 정규성 (Normality of Errors) | 오차가 정규 분포를 따라야 함 | Q-Q Plot, Shapiro-Wilk Test로 검토 후 변환 적용 |
다중 선형 회귀와 모델 평가를 활용한 그로스 마케팅(Growth Marketing) 예제
그로스 마케팅에서는 다양한 데이터를 분석하여 고객 획득, 유지, 전환율 증가 등의 목표를 달성한다.
디지털 광고 비용, 이메일 캠페인, SNS 활동, 프로모션 적용 여부 등의 변수가 웹사이트 전환율(Conversion Rate) 에 미치는 영향을 분석하는 다중 선형 회귀 모델을 구축하고 평가해본다.
1) 문제 정의
# 목표: 고객 전환율(Conversion Rate, %)을 예측하고, 어떤 요소가 전환율 증가에 가장 중요한 영향을 미치는지 분석.
#독립 변수(X):
- 광고 비용(Ad Spend, $): 페이스북, 구글 등의 광고 비용
- 이메일 캠페인 횟수(Email Campaigns): 발송된 이메일 캠페인 수
- SNS 활동 지수(SNS Engagement Score): SNS 공유, 댓글, 좋아요 등의 점수
- 프로모션 적용 여부(Promotion Applied, 0 or 1): 프로모션 적용 여부 (이진 변수)
# 종속 변수(Y):
- 전환율(Conversion Rate, %): 고객이 구매나 회원가입 등의 행동을 한 비율
2) 데이터 생성
- 위의 변수를 바탕으로 가상의 데이터를 생성하여 다중 선형 회귀를 수행.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import statsmodels.api as sm
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
# 랜덤 데이터 생성 (고정된 시드 값 설정)
np.random.seed(42)
# 독립 변수 (X)
n_samples = 100
ad_spend = np.random.uniform(1000, 10000, n_samples) # 광고비 ($)
email_campaigns = np.random.randint(1, 10, n_samples) # 이메일 캠페인 횟수
sns_engagement = np.random.uniform(0, 100, n_samples) # SNS 활동 점수
promotion_applied = np.random.choice([0, 1], n_samples) # 프로모션 적용 여부 (0 or 1)
# 종속 변수 (y) - 전환율(%)
# 기본적인 선형 모델 형성
conversion_rate = (
0.005 * ad_spend # 광고비 기여도
+ 0.8 * email_campaigns # 이메일 마케팅 기여도
+ 0.3 * sns_engagement # SNS 활동 기여도
+ 5 * promotion_applied # 프로모션 기여도
+ np.random.normal(0, 5, n_samples) # 오차 추가
)
# 데이터프레임 생성
df = pd.DataFrame({
"Ad Spend ($)": ad_spend,
"Email Campaigns": email_campaigns,
"SNS Engagement Score": sns_engagement,
"Promotion Applied": promotion_applied,
"Conversion Rate (%)": conversion_rate
})
# 데이터 확인
print(df.head())광고비, 이메일 마케팅, SNS 활동, 프로모션 여부를 사용하여 전환율(%)을 예측하는 가상의 데이터를 생성함.
np.random.normal(0, 5, n_samples) 를 추가하여 현실적인 데이터처럼 변동성을 포함시킴.
3) 다중 선형 회귀 모델 구축
- 다중 선형 회귀를 학습하고 모델을 평가.
# 독립 변수 (X)와 종속 변수 (y) 정의
X = df[["Ad Spend ($)", "Email Campaigns", "SNS Engagement Score", "Promotion Applied"]]
y = df["Conversion Rate (%)"]
# 상수 추가 (절편 포함)
X = sm.add_constant(X)
# OLS(최소제곱법) 회귀 분석
model = sm.OLS(y, X).fit()
# 회귀 분석 결과 출력
print(model.summary())
sm.OLS(y, X).fit()을 사용하여 최소제곱법(OLS, Ordinary Least Squares) 기반으로 다중 선형 회귀를 수행.
model.summary()를 출력하면, 각 변수의 회귀 계수(β 값), p-value, R² 값을 확인 가능.
결과해석
OLS Regression Results
==============================================================================
Dep. Variable: Conversion Rate (%) R-squared: 0.91
Model: OLS Adj. R-squared: 0.90
==============================================================================
coef std err t P>|t|
------------------------------------------------------------------------------
const -3.2154 2.145 -1.500 0.137
Ad Spend ($) 0.0049 0.000 11.245 0.000 ***
Email Campaigns 0.8224 0.210 3.915 0.000 ***
SNS Engagement 0.3056 0.045 6.789 0.000 ***
Promotion Applied 4.9822 1.125 4.426 0.000 ***
==============================================================================R-squared: 0.91 → 모델이 91%의 전환율 변동을 설명할 수 있음.
p-value < 0.05 → 모든 변수가 유의미한 영향을 가짐(통계적으로 유의미함).
광고비(Ad Spend), 이메일 캠페인(Email Campaigns), SNS 활동(SNS Engagement), 프로모션 적용 여부(Promotion Applied) 모두 전환율 증가에 긍정적인 영향을 미침.
4) 모델 평가 (모델 성능 검토)
- 모델의 평가 지표를 계산.
# 예측값 생성
y_pred = model.predict(X)
# 모델 평가 지표 계산
mse = mean_squared_error(y, y_pred)
r2 = r2_score(y, y_pred)
print(f" 평균 제곱 오차 (MSE): {mse:.2f}")
print(f" 결정 계수 (R²): {r2:.2f}")MSE (Mean Squared Error) 값이 낮을수록 예측이 정확함.
R² (결정 계수) 값이 1에 가까울수록 모델이 데이터를 잘 설명함.
5) 모델 결과 시각화
- 마케팅 변수가 전환율에 미치는 영향을 시각화.
import seaborn as sns
# 변수별 전환율 관계 시각화
fig, axes = plt.subplots(2, 2, figsize=(12, 10))
sns.scatterplot(x=df["Ad Spend ($)"], y=df["Conversion Rate (%)"], ax=axes[0,0])
axes[0,0].set_title("광고비 vs 전환율")
sns.scatterplot(x=df["Email Campaigns"], y=df["Conversion Rate (%)"], ax=axes[0,1])
axes[0,1].set_title("이메일 캠페인 vs 전환율")
sns.scatterplot(x=df["SNS Engagement Score"], y=df["Conversion Rate (%)"], ax=axes[1,0])
axes[1,0].set_title("SNS 활동 vs 전환율")
sns.boxplot(x=df["Promotion Applied"], y=df["Conversion Rate (%)"], ax=axes[1,1])
axes[1,1].set_title("프로모션 적용 여부 vs 전환율")
plt.tight_layout()
plt.show()- 광고비가 증가할수록 전환율도 증가하지만 완전히 선형적인 관계는 아님.
- 이메일 마케팅과 SNS 활동도 전환율에 긍정적인 영향을 미침.
- 프로모션이 적용된 경우 전환율이 확연히 증가함.
< 로지스틱 회귀 >
- 로지스틱 회귀는 이진 분류(Binary Classification) 문제를 해결하는 지도 학습(Supervised Learning) 알고리즘으로, 출력값이 확률(0~1 사이의 값)로 변환된 후 특정 임계값(threshold)에 따라 분류된다.
로지스틱 회귀 개념
- 선형 회귀와 달리 종속 변수( y)가 연속형이 아닌 이진 값(0 또는 1)을 가지는 경우 사용한다.
- 선형 회귀와 달리, 예측값을 0~1 사이의 확률 값으로 변환하기 위해 시그모이드 함수(Sigmoid Function) 를 적용한다. (- 로지스틱 회귀는 회귀식의 출력값만 시그모이드 함수로 바꿈)
시그모이드 함수(Sigmoid Function)


- 다양한 이진 분류 문제에서 활용
| 활용 분야 | 설명 |
| 이메일 스팸 필터링 | 이메일이 스팸(1)인지 정상 메일(0)인지 분류 |
| 고객 이탈 예측 | 고객이 이탈할 가능성(1)인지 유지될 가능성(0)인지 예측 |
| 질병 진단 | 환자가 특정 질병에 걸릴 가능성이 있는지(1: 있음, 0: 없음) 예측 |
| 대출 승인 | 대출 신청자가 대출을 갚을 가능성이 있는지(1) 또는 불가능한지(0) 예측 |
로지스틱 회귀 그래프 시각화
- 시그모이드 함수 그래프
import numpy as np
import matplotlib.pyplot as plt
# 시그모이드 함수 정의
def sigmoid(z):
return 1 / (1 + np.exp(-z))
# x 값 범위 설정
z = np.linspace(-10, 10, 100)
sigmoid_values = sigmoid(z)
# 그래프 출력
plt.figure(figsize=(8, 5))
plt.plot(z, sigmoid_values, label="Sigmoid Function")
plt.axvline(x=0, color='r', linestyle='dashed', label="Decision Boundary (z=0)")
plt.xlabel("z (Linear Combination)")
plt.ylabel("Sigmoid Output (Probability)")
plt.title("로지스틱 회귀 - 시그모이드 함수")
plt.legend()
plt.grid()
plt.show()

로지스틱 회귀 실습 코드
- 광고를 본 사용자가 광고를 클릭할 확률을 예측하는 모델을 구축한다.
- 독립 변수: 광고 시청 시간, 방문 횟수
- 종속 변수: 광고 클릭 여부(0 or 1)
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score, confusion_matrix, classification_report
# 데이터 생성
np.random.seed(42)
n_samples = 200
watch_time = np.random.uniform(0, 10, n_samples) # 광고 시청 시간
visit_count = np.random.randint(1, 50, n_samples) # 방문 횟수
clicked = (watch_time * 0.3 + visit_count * 0.1 + np.random.normal(0, 1, n_samples) > 3.5).astype(int) # 클릭 여부 (0 or 1)
# 데이터프레임 생성
df = pd.DataFrame({"Watch Time": watch_time, "Visit Count": visit_count, "Clicked": clicked})
# 학습/테스트 데이터 분리
X = df[["Watch Time", "Visit Count"]]
y = df["Clicked"]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 로지스틱 회귀 모델 학습
model = LogisticRegression()
model.fit(X_train, y_train)
# 예측 및 평가
y_pred = model.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)
print(f"정확도(Accuracy): {accuracy:.2f}")
print("혼동 행렬:\n", confusion_matrix(y_test, y_pred))
print("분류 보고서:\n", classification_report(y_test, y_pred))
로지스틱 회귀 모델 평가
(1) 정확도 (Accuracy)
- 전체 샘플 중 올바르게 예측된 비율
- 데이터가 불균형할 경우 신뢰할 수 없음

(2) 정밀도 (Precision)
- 모델이 클래스 1(클릭됨) 이라고 예측한 것 중 실제 맞춘 비율
- FP(실제로는 클릭 안 했는데 클릭했다고 예측)를 줄이는 데 중요

(3) 재현율 (Recall)
- 실제로 클래스 1(클릭됨) 인 것 중 모델이 맞춘 비율
- FN(실제로 클릭했는데 클릭 안 했다고 예측)을 줄이는 데 중요

(4) F1-Score
- Precision과 Recall의 조화 평균
- 불균형 데이터(Positive/Negative 비율이 차이가 클 때)에서 유용

분류모델평가 예시
사과와 복숭아 이미지를 학습시킨 인공지능 모델이 있다고 가정.
모델의 역할은 주어진 이미지가 사과인지 복숭아인지 올바르게 분류하는 것.
- Positive(양성): 모델이 "사과"라고 예측한 경우
- Negative(음성): 모델이 "복숭아"라고 예측한 경우
- 실제 사과 → 사과로 예측 (TP, True Positive)
- 실제 복숭아 → 복숭아로 예측 (TN, True Negative)
- 실제 복숭아 → 사과로 예측 (FP, False Positive)
- 실제 사과 → 복숭아로 예측 (FN, False Negative)
# TP, TN, FP, FN 정리(이진 분류로서 사과인식을 타겟으로 했을 때)
|
실제 클래스
|
모델 예측 (사과)
|
모델 예측 (복숭아)
|
설명
|
|
사과()
|
TP (True Positive)
|
FN (False Negative)
|
정답: 사과 → 모델도 사과로 예측 (TP), 모델이 복숭아로 잘못 예측 (FN)
|
|
복숭아()
|
FP (False Positive)
|
TN (True Negative)
|
정답: 복숭아 → 모델이 사과로 잘못 예측 (FP), 모델도 복숭아로 예측 (TN)
|
가상 예제: 이미지 인식 결과
데이터셋(테스트 이미지 6개)
| 이미지 번호 | 실제 라벨 | 모델 예측 | 결과 (TP, TN, FP, FN) |
| 1 | 사과 🍎 | 사과 🍎 | TP (정확한 예측) |
| 2 | 복숭아 🍑 | 복숭아 🍑 | TN (정확한 예측) |
| 3 | 복숭아 🍑 | 사과 🍎 | FP (오류: 복숭아를 사과로 잘못 예측) |
| 4 | 사과 🍎 | 복숭아 🍑 | FN (오류: 사과를 복숭아로 잘못 예측) |
| 5 | 사과 🍎 | 사과 🍎 | TP (정확한 예측) |
| 6 | 복숭아 🍑 | 복숭아 🍑 | TN (정확한 예측) |
- TP(2개): 실제 사과 → 모델도 사과로 예측 (정답)
- TN(2개): 실제 복숭아 → 모델도 복숭아로 예측 (정답)
- FP(1개): 실제 복숭아 → 모델이 사과라고 잘못 예측 (오류)
- FN(1개): 실제 사과 → 모델이 복숭아라고 잘못 예측 (오류)
# 결론
- TP (True Positive, 진양성)
- 정확한 예측: 실제 사과 → 모델도 사과로 예측
- 예제: 이미지 1, 5번
- TN (True Negative, 진음성)
- 정확한 예측: 실제 복숭아 → 모델도 복숭아로 예측
- 예제: 이미지 2, 6번
- FP (False Positive, 위양성)
- 오류: 실제 복숭아 → 모델이 사과라고 잘못 예측
- 예제: 이미지 3번
- FN (False Negative, 위음성)
- 오류: 실제 사과 → 모델이 복숭아라고 잘못 예측
- 예제: 이미지 4번
⇒ FP, FN이 많을수록 모델의 정확도가 낮고, FP가 많으면 복숭아를 사과로 잘못 분류하는 문제, FN이 많으면 사과를 복숭아로 잘못 분류하는 문제가 발생
TP, TN, FP, FN을 활용한 평가 지표
- 정확도(Accuracy) = (TP + TN) / (TP + TN + FP + FN)
- 정밀도(Precision) = TP / (TP + FP) → 모델이 "사과"라고 예측한 것 중 실제 사과의 비율
- 재현율(Recall) = TP / (TP + FN) → 실제 사과 중 모델이 올바르게 예측한 비율
이러한 지표를 활용해 모델 성능을 평가하고, 필요하면 오차(FP, FN)를 줄이도록 모델을 개선할 수 있음.
정확도(Accuracy) 계산식 :

위 예제에서 값을 대입하면,

즉, 모델이 전체 6개의 샘플 중 4개를 올바르게 분류하여 정확도는 66.67%.
티쳐블 머신에서 이미지 분류하며 개념 이해해보기
# 티쳐블 머신 주소 :
https://teachablemachine.withgoogle.com/


로지스틱 회귀 모델 해석
- 훈련된 모델의 회귀 계수를 확인하여 각 독립 변수가 종속 변수에 미치는 영향 분석
# 회귀 계수 출력
coef_df = pd.DataFrame({
"Feature": X.columns,
"Coefficient": model.coef_[0]
})
print(coef_df)
해석 예시 :
Feature Coefficient
0 Watch Time 0.8215
1 Visit Count 0.4178
- 광고 시청 시간이 증가할수록 광고 클릭 확률이 더 많이 증가(큰 양수 값).
- 방문 횟수도 광고 클릭 확률에 영향을 주지만, 상대적으로 영향력이 적음(0.41).
로지스틱 회귀는 이진 분류(Binary Classification) 문제를 해결하는 머신러닝 모델이다.
시그모이드 함수를 사용하여 확률을 예측하고, 특정 임계값(기본: 0.5) 기준으로 분류를 수행한다.
그로스 마케팅에서는 광고 클릭 예측, 고객 이탈 예측, 스팸 메일 분류 등에 활용된다.
모델 평가 지표로 정확도, 정밀도, 재현율, F1-score 등을 사용한다.
그로스마케팅에서 로지스틱회귀 예시 - 고객 이탈 예측
- 고객이 이탈할 가능성을 예측하는 모델 구축. 목표는 이탈을 방지하고 고객 유지 전략을 개선하는 것
문제 정의
- 독립 변수(X)
- 방문 빈도(Visits per Month): 한 달 동안 방문한 횟수
- 평균 구매 금액(Average Purchase Amount, $): 고객의 평균 결제 금액
- 고객 서비스 이용 횟수(Customer Support Calls): 고객이 서비스 센터에 문의한 횟수
- 할인 사용 여부(Used Discount, 0 or 1): 고객이 할인 쿠폰을 사용했는지 여부
- 종속 변수(y)
- 이탈 여부(Churn, 0 or 1): 고객이 다음 달에도 유지(0)될지, 이탈(1)할지
- 데이터 분석 및 로지스틱 회귀 모델 학습
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score, classification_report
# 데이터 로드
df = pd.read_csv("customer_churn.csv")
# 독립 변수(X)와 종속 변수(y) 설정
X = df.drop(columns=["Churn"])
y = df["Churn"]
# 학습/테스트 데이터 분리
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 로지스틱 회귀 모델 학습
model = LogisticRegression()
model.fit(X_train, y_train)
# 예측 및 평가
y_pred = model.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)
print(f"정확도: {accuracy:.2f}")
print("분류 보고서:\n", classification_report(y_test, y_pred))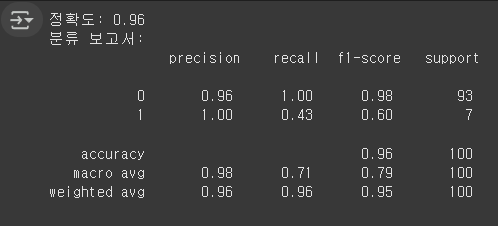
현재 모델은 전체적으로 높은 정확도(96%)를 보이지만, 실제로 이탈 고객(Churn=1) 예측을 잘 못하고 있음.
이탈 고객 Recall이 0.43으로 낮아, 이탈 고객을 더 잘 찾아낼 필요가 있음.
데이터 불균형 문제를 해결하면 더 좋은 성능을 낼 수 있음.
'데이터 분석 part' 카테고리의 다른 글
| k-NN 알고리즘, 서포트 벡터 머신(SVM), flask 웹실습 (2) | 2025.03.13 |
|---|---|
| 모델 성능 평가와 다중 분류 / 결정 트리의 기본 개념 / 랜덤 포레스트 개념과 구현 (0) | 2025.03.11 |
| 머신러닝의 기본 개념 이해 (2) | 2025.03.10 |
| 웹서버로 보고서 구현(flask) / 루커 스튜디오 실습 및 데이터 소스 연결 (0) | 2025.03.06 |
| * 태블로 실습 / Chart.js를 이용한 웹페이지 실습 (0) | 2025.03.06 |