지난 수업 예제
코드 ( 광고비와 판매량 사이의 관계를 선형회귀분석으로 분석)
# statsmodels - 통계분석 라이브러리
# numpy - 숫자를 다루기 위한 라이브러리
import statsmodels.api as sm
import numpy as np
# 독립변수(광고비)와 종속변수(판매량) 예제 데이터
# np.array()를 써서 데이터를 숫자로 다루기 쉽게 한다.
X = np.array([1, 2, 3, 4, 5]) # 광고비(독립변수)
Y = np.array([3, 6, 7, 8, 11]) # 판매량(종속변수)
# 상수항 추가
# 상수항(절편)(b)을 추가하는 코드
# sm.OLS() 같은 함수는 절편을 따로 수동으로 추가해줘야 함.
X = sm.add_constant(X)
# 선형 회귀 모델 학습
# sm.OLS(Y, X).fit()는 "최소제곱법(OLS)"으로 회귀 모델을 학습하는 코드.
# Y는 종속변수(판매량)
# X는 독립변수 (광고비 + 상수항)
# .fit(): 데이터를 학습해서 최적의 선형 회귀식을 찾음.
model = sm.OLS(Y, X).fit()
# 회귀 분석 결과 출력
# model.summary()는 회귀 분석 결과(기울기, 절편, p-value, R² 등)를 보여주는 코드.
print(model.summary())
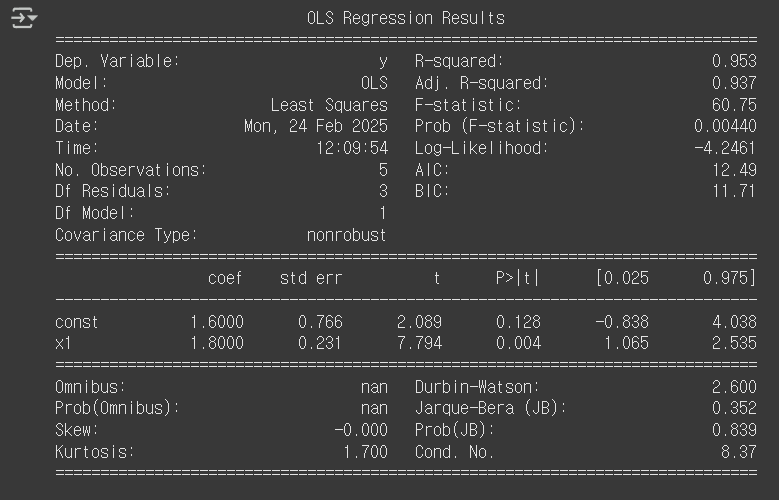
결과:
# R² 값이 0.953이니까, 이 모델이 판매량(Y)을 95.3% 설명할 수 있다는 뜻.
(즉, 광고비(X)와 판매량(Y) 사이의 관계가 아주 강하다는 의미) R²이 1에 가까울수록 모델이 데이터를 잘 설명.
(Adjusted R² (0.937)도 높은데, 이 값은 독립변수(광고비)의 개수를 고려해서 보정된 결정계수)
독립변수가 많아지면 R²는 커지지만, Adjusted R²는 의미 없는 변수에는 벌점을 줘서 더 신뢰할 수 있음.
# const (절편): 1.6 → 광고비가 0원일 때, 예상 판매량이 1.6이라는 뜻
# x1 (광고비의 기울기): 1.8

# P>|t| (절편): 0.128 (유의하지 않음) → 절편(const)의 P-value ≥ 0.05 - 절편은 통계적으로 유의하지 않음.
# P>|t| (광고비의 기울기): 0.004 (유의함) → 광고비 (x1)의 P-value < 0.05 - 광고비는 판매량에 유의한 영향을 준다.
# Prob (F-statistic) = 0.00440 → 회귀식 전체의 유의성을 나타내는 값
0.00440 < 0.05 → 회귀식이 전체적으로 유의하다. (즉, 광고비가 판매량을 잘 설명함)
# Durbin-Watson: 2.600 - 잔차 분석 : 잔차(오차)들이 독립적인지 확인
1.5 ~2.5 사이면 괜찮고, 2에 가까울수록 좋다. 2.6이면 약간 크지만 크게 문제될 정도는 아님.
※ 최소제곱법(OLS)이란?
최소제곱법(OLS)은 회귀 분석에서 가장 많이 사용하는 방법으로, 오차(잔차, Residuals)의 제곱합을 최소화하는 방식으로 최적의 회귀선을 찾는 방법.
OLS는 가장 적절한 직선을 찾는 방법이고, statsmodels에서 sm.OLS()를 사용하면
자동으로 최소제곱법을 적용해서 최적의 회귀선을 계산.
※ sm.OLS() 같은 함수는 상수항(절편)을 따로 추가하지 않으면 자동으로 계산하지 않기 때문에, 수동으로 상수항(절편)을 X에 추가해줘야 함. sklearn.linear_model.LinearRegression() 함수에서는 상수항(절편)을 자동으로 포함시켜 모델을 학습시켜줌.
코드 ( stats.pearsonr()를 이용한 상관 분석 ) - 위의 코드랑 이어지는 코드
- 광고비(X)와 판매량(Y) 사이의 관계를 알아보기 위해 '피어슨 상관계수'를 계산하는 코드.
# scipy.stats 라이브러리를 불러옴.
# 이 안에 있는 stats.pearsonr() 함수를 사용해서 두 변수 간의 상관계수를 계산
from scipy import stats
# 독립변수(광고비)와 종속변수(판매량)
# 두 변수 간의 상관계수 계산
# 피어슨 상관계수(상관도)와 p-value(유의확률)를 계산하는 부분
# X[:, 1]: X가 2차원 배열(예: [[1, 2], [3, 4], [5, 6]])일 때, 두 번째 열(광고비)을 가져옴.
# Y: 종속변수(판매량)
# 두 변수(X와 Y) 간의 상관관계(r 값)와 p-value(통계적 유의미성)를 계산.
correlation_coefficient, p_value = stats.pearsonr(X[:, 1], Y)
#상관계수(correlation_coefficient)와 p-값(p_value)을 출력.
print(f"상관계수: {correlation_coefficient}")
print(f"P-값: {p_value}")
# p-value를 기준으로 결과를 해석
if p_value < 0.05:
print("두 변수 간 상관관계가 통계적으로 유의미함")
else:
print("두 변수 간 상관관계가 통계적으로 유의미하지 않음")
- 상관계수 (r 값)
- 1에 가까울수록 강한 양의 상관관계 (광고비 증가 → 판매량 증가)
- -1에 가까울수록 강한 음의 상관관계 (광고비 증가 → 판매량 감소)
- 0에 가까우면 상관관계가 거의 없음
- p-value (유의확률)
- p-value < 0.05 → 상관관계가 통계적으로 유의미함 (신뢰할 수 있음)
- p-value ≥ 0.05 → 상관관계가 통계적으로 유의미하지 않음 (우연일 가능성이 큼)

결과:
상관계수(r) = 0.9761 은 거의 1에 가까운 값. 강한 상관관계.
즉, 광고비(X)가 증가할수록 판매량(Y)도 거의 비례해서 증가한다는 의미.
P-value = 0.004 → 0.05보다 작으므로 통계적으로 유의미함.
광고비와 판매량 사이의 상관관계가 우연이 아닐 가능성이 높고, 실제로 연관성이 있다고 볼 수 있음.
회귀분석이란?
- 두 개 이상의 변수 사이의 관계를 분석하고 예측 모델을 구축하는 기법.
- 주어진 데이터로부터 변수 간의 상관관계를 파악하고, 이를 바탕으로 미래의 값을 예측하거나 변수들이 어떻게 상호작용하는지 이해하는데 사용
회귀분석의 개념
주요 구성 요소
# 종속변수 (label) - Y
- 분석의 목표가 되는 변수
- 알고싶은 항목
# 독립변수 - X
- 종속변수에 영향을 주는 변수
# 오차항 (입실론)
- 실제값에서 추정값을 뺀 값. (측정오차나 누락된 변수 등)


회귀모델의 형태
- 선형(linear) 또는 비선형(nonlinear) 형태
- 대표적인 방법으로 최소제곱법(OLS, R-Squared)을 사용하여 모델의 파라미터를 추정
단순회귀분석
- 하나의 독립변수와 하나의 종속변수 사이의 선형관계
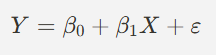

최소제곱법 (OLS, R-Squared)
- 단순회귀분석에서는 최소제곱법을 통해 절편과 기울기를 추정.
- 각 관측치에서 예측값과 실제값 사이의 잔차의 제곱합을 최소화하는 파라미터를 찾는 방법
→ 에러를 0으로 수렴시키겠다.
회귀분석의 기본 가정
# 선형성
- 직선이어야 한다.
※ 데이터가 선형적이지 않을 경우 비선형 변환이나 다른 모델링 기법 필요
# 독립성
- 각 관측치가 서로 독립적이어야 함
# 등분산성 (같은 간격)
- 모든 수준의 독립 변수에서 오차의 분산이 동일하다는 가정
# 정규성
- 오차항이 정규분포를 따른다는 가정
모델 적합도 평가 및 검정
결정계수 (R²)
- 0과 1사이의 값을 가지며, 1에 가까울수록 회귀 모델의 설명력이 좋음을 의미
(0이면 모델이 평균값만큼도 설명하지 못한다는 뜻. 음수가 나오면 그 모델은 심히 안좋다.)
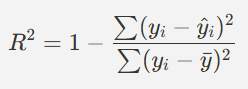
결정계수는 1에서 오차 제곱합(RSS)을 총 제곱합(TSS)으로 나눈 값을 빼는 방식으로 계산.

t-검정 및 p-값
- t-검정: 각 회귀계수가 통계적으로 유의한지를 검정.
- p-값: 기울기나 절편이 0이라는 귀무가설을 기각할 수 있는지 판단. 일반적으로 p-값이 0.05 미만이면 유의하다고 봄.
F-검정
- 전체 모델의 유의성을 검정하는 방법으로, 독립 변수가 종속 변수의 변동을 설명하는 데 유의한지 평가.
※ 유의사항
- 회귀분석은 변수간 상관관계를 분석하지만 인과관계를 확정하지는 않음
- 선형성, 독립성, 등분산성, 정규성 등의 가정이 위배되면 모델의 추정치와 해석에 문제발생할 수 있음
- 중요한 독립변수가 누락되면 결과가 왜곡될 수 있음
- 이상치는 회귀계수 추정에 큰 영향을 미칠 수 있으므로, 데이터 전처리와 이상치 처리가 필요
단순 회귀분석 예시 코드
import numpy as np # numpy는 수치계산, 대규모 배열 및 행렬 다루는 라이브러리
import pandas as pd # pandas : 데이터분석 라이브러리
import matplotlib.pyplot as plt # 그래프 시각화 라이브러리
from sklearn.linear_model import LinearRegression # 선형회귀모델 사용하는 라이브러리
from sklearn.metrics import r2_score # 결정계수 계산하는 라이브러리
# 1. 가상의 데이터 생성
# np.random.seed(42): 랜덤 값을 고정해서 실행할 때마다 같은 값이 나오도록 설정.
np.random.seed(42) # 결과 재현을 위한 시드 설정
# 광고비 데이터: 1,000 ~ 10,000 달러 사이의 50개 포인트
# np.linspace(1000, 10000, 50): 광고비 데이터를 1000~10000 사이에서 50개 생성.
ad_spend = np.linspace(1000, 10000, 50)
# 실제 전환수: 실제로는 광고비가 증가할수록 전환수가 증가한다고 가정
# 실제 모형: conversions = intercept + slope * ad_spend + noise
# true_intercept = 50: 광고비가 0일 때 전환수가 50.
true_intercept = 50
# true_slope = 0.05: 광고비가 1달러 증가할 때 전환수가 0.05 증가.
true_slope = 0.05
# noise = np.random.normal(0, 30, ad_spend.shape[0]): 전환수에 노이즈(랜덤 값)를 추가해서 현실적인 데이터처럼 보이게 만듬.
noise = np.random.normal(0, 30, ad_spend.shape[0]) # 랜덤 노이즈 추가
# conversions = true_intercept + true_slope * ad_spend + noise: 광고비에 따라 전환수를 계산.
conversions = true_intercept + true_slope * ad_spend + noise
# 데이터프레임 생성
# pandas.DataFrame을 이용해 광고비(ad_spend)와 전환수(conversions) 데이터를 표로 만듬.
df = pd.DataFrame({'ad_spend': ad_spend, 'conversions': conversions})
# 2. 회귀분석을 위한 데이터 준비
# X = df[['ad_spend']]: 광고비를 독립 변수로 설정.
# y = df['conversions']: 전환수를 종속 변수로 설정.
X = df[['ad_spend']] # 독립 변수 (광고비)
y = df['conversions'] # 종속 변수 (전환수)
# 3. 단순 회귀 모델 생성 및 학습
# LinearRegression(): 선형 회귀 모델을 만든다.
# model.fit(X, y): 광고비(X)를 이용해서 전환수(y)를 예측하도록 모델을 학습시킨다.
model = LinearRegression()
model.fit(X, y)
# 4. 모델 파라미터 출력
# model.intercept_: 모델이 학습한 절편 (광고비가 0일 때 예상 전환수).
# model.coef_[0]: 모델이 학습한 기울기 (광고비가 1달러 증가할 때 전환수 증가량).
print("모델 절편 (Intercept):", model.intercept_)
print("모델 기울기 (Slope):", model.coef_[0])
# 5. 예측값 계산 및 결정계수 평가
# model.predict(X): 학습한 모델을 이용해 전환수를 예측.
# r2_score(y, y_pred) : 결정계수를 계산. r2값이 1에 가까울 수록 모델이 데이터를 잘 설명하는 것.
y_pred = model.predict(X)
print("결정계수 (R²):", r2_score(y, y_pred))
# 6. 결과 시각화
# 파란 점 : 실제 데이터.
# 빨간 선 : 회귀 모델이 예측한 선.
plt.scatter(df['ad_spend'], df['conversions'], color='blue', label='실제 데이터')
plt.plot(df['ad_spend'], y_pred, color='red', label='회귀 직선')
plt.title('광고비 대비 전환수 분석')
plt.xlabel('광고비 ($)')
plt.ylabel('전환수')
plt.legend()
plt.show()
# 광고비가 증가할수록 전환수가 증가한다.
# 절편 : 광고비가 0일때 예상 전환수는 약 53.87명
# 기울기 : 광고비가 1달러 증가할 때 전환수는 0.0481명 증가
# 결정계수 : 0.956이므로 1에 가까우므로 모델이 데이터를 잘 설명.
단순회귀분석 문제 풀기 코드
# 문제1,2,3 코드
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
# 1. 주어진 데이터
# 광고비와 전환수 데이터를 numpy 배열로 저장함.
ad_spend = np.array([1000, 3000, 5000, 7000, 9000]) # 광고비 (독립 변수)
conversions = np.array([105, 195, 310, 395, 505]) # 전환수 (종속 변수)
# 데이터프레임 생성
# pandas.DataFrame()을 이용해 데이터프레임(df) 형태로 변환.
# 독립변수(X) → 광고비
# 종속변수(Y) → 전환수
df = pd.DataFrame({'ad_spend': ad_spend, 'conversions': conversions})
# 2. 회귀분석을 위한 데이터 준비
# X = df[['ad_spend']] → 독립변수(광고비)를 2차원 배열 형태로 준비 (대괄호 2개 [[ ]] )
# y = df['conversions'] → 종속변수(전환수)를 1차원 배열로 저장
X = df[['ad_spend']] # 독립 변수 (광고비)
y = df['conversions'] # 종속 변수 (전환수)
# 3. 단순 회귀 모델 생성 및 학습
# LinearRegression().fit(X, y) → 광고비와 전환수 사이의 관계를 학습
model = LinearRegression()
model.fit(X, y)
# 4. 모델 파라미터 출력
# model.intercept_ → 절편(β₀), 즉 X=0일 때 예상되는 Y 값
# model.coef_[0] → 기울기(β₁), 즉 광고비가 1 증가할 때 전환수가 얼마나 증가하는지
print("모델 절편 (Intercept):", model.intercept_)
print("모델 기울기 (Slope):", model.coef_[0])
# 5. 예측값 계산 및 결정계수 평가
# model.predict(X) → 학습한 모델을 이용해 주어진 광고비 데이터(X)에 대해 예측된 전환수(y_pred)를 계산.
# r2_score(y, y_pred) → 실제 값(y)과 예측값(y_pred)의 일치 정도 (결정계수인 R² 값) 확인
y_pred = model.predict(X)
print("결정계수 (R²):", r2_score(y, y_pred))
# ad_spend_new = np.array([[6000]]) : 예측할 광고비를 넘파이 배열 형태로 저장
# [[6000]] → 2차원 배열로 변환해야 sklearn의 predict() 함수가 정상적으로 동작함
# predicted_conversion = model.predict(ad_spend_new) : 학습된 회귀 모델(model)을 사용해 광고비 6000달러일 때 전환수를 예측
# predict() 함수는 입력된 광고비를 기반으로 회귀 방정식을 적용하여 전환수를 계산
# predicted_conversion[0] → 예측된 값은 배열 형태이므로 [0]으로 첫 번째 값을 가져옴
# .2f → 소수점 둘째 자리까지 출력
ad_spend_new = np.array([[6000]]) # 예측할 광고비 (2차원 배열 형태)
predicted_conversion = model.predict(ad_spend_new) # 예측
print(f"광고비 6000달러일 때 예상 전환수: {predicted_conversion[0]:.2f}")
# 6. 결과 시각화
# 파란색 점 (산점도) → 실제 광고비 & 전환수 데이터
# 빨간색 선 (회귀선) → 학습한 회귀 모델이 예측한 값
plt.scatter(df['ad_spend'], df['conversions'], color='blue', label='실제 데이터')
plt.plot(df['ad_spend'], y_pred, color='red', label='회귀 직선')
plt.title('광고비 대비 전환수 분석')
plt.xlabel('광고비 ($)')
plt.ylabel('전환수')
plt.legend()
plt.show()
# y = 52 + 0.05x
# 광고비 6000달러를 투자할때 예상되는 전환수는 352명이다.
# 결정계수는 0.998이므로 거의 1에 가까운 값이다. 모델이 데이터를 잘 설명해주고 있다.
# 따라서 광고비가 전환수에 영향을 미치므로 광고비를 늘리는 것도 좋은 방안이다.
※ 데이터 중 일부에 이상치가 존재한다면?
- 노이즈에 이상치를 집어넣는다.
단순회귀분석 예시코드 (보고서 작성용)
# 보고서 작성용 예시 코드
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
# 1. 가상의 데이터 준비
data = {
'ad_spend': [1000, 2000, 3000, 4000, 5000, 6000, 7000, 8000, 9000, 10000],
'conversions': [120, 150, 180, 210, 240, 265, 290, 320, 345, 370]
}
df = pd.DataFrame(data)
# 2. 독립 변수(X)와 종속 변수(y) 설정
X = df[['ad_spend']]
y = df['conversions']
# 3. 단순 회귀 모델 생성 및 학습
model = LinearRegression()
model.fit(X, y)
# 4. 모델 파라미터 및 결정계수(R²) 출력
intercept = model.intercept_
slope = model.coef_[0]
r2 = r2_score(y, model.predict(X))
print("회귀식: 전환수 = {:.2f} + {:.5f} * 광고비".format(intercept, slope))
print("결정계수 (R²): {:.4f}".format(r2))
# 5. 예측 및 시각화
df['predicted_conversions'] = model.predict(X)
plt.scatter(df['ad_spend'], df['conversions'], color='blue', label='실제 전환수')
plt.plot(df['ad_spend'], df['predicted_conversions'], color='red', label='회귀 직선')
plt.title('광고비 대비 전환수 분석')
plt.xlabel('광고비 ($)')
plt.ylabel('전환수')
plt.legend()
plt.show()
※ 상관계수와 결정계수의 차이
| 지표 | 의미 | 값 범위 | 목적/용도 |
| 상관계수 | 두 변수 간의 선형 관계의 강도와 방향을 나타냄 | -1 ~ 1 | 두 변수 간의 관계를 이해하고, 상관도을 평가 |
| 결정계수 (R²) | 회귀 모델이 종속 변수의 변동을 얼마나 잘 설명하는지 평가 | 0 ~ 1 | 회귀 모델의 설명력을 평가 |
다중 회귀 분석
- 하나의 종속 변수와 두 개 이상의 독립 변수간의 관계를 동시에 분석.
- 마케팅에서는 여러 요인이 매출에 미치는 영향을 동시에 분석 가능.


# 최소제곱법(OLS, R-Squared) :
- 관측된 데이터와 모델에 의한 예측 값 사이의 잔차 제곱합을 최소화하는 방법
→ 에러를 0으로 수렴하게...
# 결정계수 :
- 모델이 종속변수의 변동성을 얼마나 설명하는지 나타냄. 0과 1사이의 값

※ 결정계수가 1이라면 ??? → 과적합을 의심해 봐야된다.
모델이 훈련 데이터에 너무 잘 맞춰져서 새로운 데이터(테스트 데이터)에는 잘 일반화되지 않는 상태일 수 있음.
# 조정된 결정계수 :
- 독립 변수의 개수가 늘어날 때 발생할 수 있는 과적합 문제를 보정하기 위해 사용.
# F-검정:
- 전체 모델의 유의성을 평가하여, 적어도 하나의 독립 변수가 종속 변수와 유의한 관계가 있는지를 검정.
다중 회귀 분석의 기본 가정
# 선형성
# 독립성
# 등분산성
# 정규성
# 다중 공선성
- 독립 변수들 간에 높은 상관관계가 존재하면 계수 추정의 불안정성이 발생할 수 있음.
다중 회귀 분석의 장점과 한계
- 장점 : 단순회귀분석보다 복합 요인 분석과 예측력이 향상된다는 것
- 단점 : 모형복잡성, 다중공선성 문제, 가정 위배
다중회귀분석 예시 코드
#필요한 라이브러리 불러오기
# numpy: 수학 연산을 다룰 때 사용하는 라이브러리로, 여기선 데이터 생성과 무작위 값 생성을 위해 사용.
# pandas: 데이터를 다룰 때 매우 유용한 라이브러리로, 데이터프레임 형태로 데이터를 처리할 수 있음.
# matplotlib.pyplot: 데이터를 시각화(그래프 그리기)하는 라이브러리로, 데이터를 보기 좋게 그래프나 차트로 그릴 때 사용.
# sklearn.linear_model.LinearRegression: 선형 회귀 모델을 만들기 위한 라이브러리.
# sklearn.metrics.r2_score: 모델의 성능을 평가할 때 쓰는 결정계수(R²)를 계산하는 함수.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
# 가상의 데이터 생성
# 예: 매출(Y)은 광고비(X1)와 프로모션 예산(X2)의 영향을 받음
# np.random.seed(42): 이 코드를 실행할 때마다 같은 값을 생성할 수 있도록 하는 "시드"를 설정.
# ad_spend: 광고비 데이터를 1,000에서 10,000 달러 사이의 값으로 50개 포인트 생성.
# promo_budget: 프로모션 예산 데이터를 500에서 5,000 달러 사이의 값으로 50개 포인트 생성.
np.random.seed(42)
n = 50
ad_spend = np.random.uniform(1000, 10000, n) # 광고비 (달러)
promo_budget = np.random.uniform(500, 5000, n) # 프로모션 예산 (달러)
# 실제 모델: Y = 50 + 0.03*ad_spend + 0.05*promo_budget + noise
# noise: 데이터에 랜덤 노이즈를 추가하여 현실적인 데이터의 변동성을 나타냄.
# 최종적으로 sales는 실제 매출 값을 생성하는 코드
true_intercept = 50
true_coef_ad = 0.03
true_coef_promo = 0.05
noise = np.random.normal(0, 30, n)
sales = true_intercept + true_coef_ad * ad_spend + true_coef_promo * promo_budget + noise
# 데이터프레임 생성
# pandas의 DataFrame을 사용하여, ad_spend, promo_budget, sales를 하나의 표 형태로 묶음.
df = pd.DataFrame({
'ad_spend': ad_spend,
'promo_budget': promo_budget,
'sales': sales
})
# 독립 변수와 종속 변수 설정
# X는 독립 변수로, 광고비와 프로모션 예산이 포함된 데이터셋.
# y는 종속 변수로, 매출을 나타냄.
X = df[['ad_spend', 'promo_budget']]
y = df['sales']
# 다중 회귀 모델 생성 및 학습
# LinearRegression()을 사용하여 선형 회귀 모델을 생성.
# fit()을 사용하여 모델을 학습시킴. 이 때, 광고비와 프로모션 예산을 기반으로 매출을 예측하는 모델을 학습함.
model = LinearRegression()
model.fit(X, y)
# 모델 파라미터 및 결정계수 출력
# model.intercept_: 절편 값 (기본값 50)
# model.coef_[0]: 광고비에 대한 기울기 (0.03)
# model.coef_[1]: 프로모션 예산에 대한 기울기 (0.05)
# r2_score(): 결정계수(R²)를 출력. 모델이 얼마나 잘 데이터를 설명하는지 나타내는 지표.
print("회귀식: 매출 = {:.2f} + {:.5f} * 광고비 + {:.5f} * 프로모션 예산".format(
model.intercept_, model.coef_[0], model.coef_[1]
))
print("결정계수 (R²): {:.4f}".format(r2_score(y, model.predict(X))))
# 산점도와 회귀면 시각화(2차원 시각화는 독립 변수가 2개이므로 다소 복잡할 수 있음)
# 여기서는 광고비에 따른 예측 매출을 예시로 시각화합니다.
# 파란점 : 실제 매출 / 빨간점 : 예측된 매출
plt.scatter(df['ad_spend'], y, color='blue', label='실제 매출')
plt.scatter(df['ad_spend'], model.predict(X), color='red', label='예측 매출', alpha=0.5)
plt.xlabel('광고비 ($)')
plt.ylabel('매출')
plt.title('광고비 대비 매출 예측 (프로모션 예산 고려)')
plt.legend()
plt.show()
- 절편 (75.84): 광고비와 프로모션 예산이 모두 0일 때, 기본 매출이 약 75.84 달러.
- 광고비의 기울기 (0.02557): 광고비가 1달러 증가할 때, 매출은 0.02557 달러 증가.
- 프로모션 예산의 기울기 (0.04888): 프로모션 예산이 1달러 증가할 때, 매출은 0.04888 달러 증가.
- 결정계수 값이 0.9350이라는 것은 모델이 매출의 변동을 약 93.5% 정도 설명 (모델이 잘 작동)
다중회귀분석 예시코드2
# numpy: 수학적 계산을 할 때 사용하는 라이브러리로, 주로 배열 연산에 사용됨.
# pandas: 데이터 처리 및 분석에 유용한 라이브러리로, 테이블 형태(데이터프레임)로 데이터를 다룰 수 있음.
# matplotlib.pyplot: 그래프를 그릴 때 사용하는 라이브러리. 데이터를 시각적으로 표현할 때 필요.
# sklearn.linear_model.LinearRegression: 선형 회귀 모델을 사용하기 위한 클래스. 데이터를 기반으로 예측 모델을 만들 때 사용.
# sklearn.metrics.r2_score: 모델의 성능을 평가할 때 쓰는 결정계수(R²)를 계산하는 함수.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
# 1. 가상의 데이터 준비
# data: ad_spend, promo_budget,website_traffic(3개의 독립변수), sales(종속변수)에 대한 데이터가 들어 있는 딕셔너리.
# 이 데이터를 pandas의 데이터프레임으로 변환해서 df라는 이름의 표로 저장함.
data = {
'ad_spend': [1000, 2000, 3000, 4000, 5000, 6000, 7000, 8000, 9000, 10000],
'promo_budget': [500, 700, 900, 1100, 1300, 1500, 1700, 1900, 2100, 2300],
'website_traffic': [2000, 2500, 3000, 3500, 4000, 4500, 5000, 5500, 6000, 6500],
'sales': [15000, 18000, 22000, 25000, 29000, 32000, 36000, 40000, 44000, 48000]
}
df = pd.DataFrame(data)
# 2. 독립 변수와 종속 변수 설정
# 독립변수인 ad_spend, promo_budget, website_traffic 이 3개의 변수를 사용해서 매출을 예측.
# 종속 변수인 sales는 예측하려는 대상(알고싶은 값)
X = df[['ad_spend', 'promo_budget', 'website_traffic']]
y = df['sales']
# 3. 다중 회귀 모델 생성 및 학습
# LinearRegression(): 선형 회귀 모델을 만드는 클래스.
# model.fit(X, y): 모델을 학습하는 부분. 주어진 독립 변수(X)를 바탕으로 종속 변수(y)를 예측하는 방법을 학습.
model = LinearRegression()
model.fit(X, y)
# 4. 회귀식과 및 결정계수(R²) 출력
# 회귀식: model.intercept_는 절편(Intercept), model.coef_는 기울기(coefficient)를 나타냄.
# 결정계수(R²): r2_score(y, model.predict(X))는 모델이 실제 매출을 얼마나 잘 예측하는지를 평가하는 값.
print("회귀식: 매출 = {:.2f} + {:.5f} * 광고비 + {:.5f} * 프로모션 예산 + {:.5f} * 웹사이트 방문자 수".format(
model.intercept_, model.coef_[0], model.coef_[1], model.coef_[2]
))
print("결정계수 (R²): {:.4f}".format(r2_score(y, model.predict(X))))
# 5. 예측 결과: 실제 매출과 예측 매출 비교
# predicted_sales = model.predict(X): 모델을 이용해 예측된 매출.
# plt.scatter(y, predicted_sales, color='blue'): 실제 매출과 예측된 매출을 비교하는 산점도 그래프.
# 대각선(y=x): 빨간색 대각선은 실제 매출과 예측 매출이 완전히 일치하는 상태를 나타냄.
predicted_sales = model.predict(X)
plt.figure(figsize=(8, 6))
plt.scatter(y, predicted_sales, color='blue', label='예측 매출')
plt.plot([min(y), max(y)], [min(y), max(y)], color='red', linestyle='--', label='대각선 (y=x)')
plt.xlabel('실제 매출 (달러)')
plt.ylabel('예측 매출 (달러)')
plt.title('실제 매출 vs 예측 매출')
plt.legend()
plt.show()
- model.coef_[0]는 광고비(ad_spend)에 대한 기울기
- model.coef_[1]은 프로모션 예산(promo_budget)에 대한 기울기
- model.coef_[2]는 웹사이트 방문자 수(website_traffic)에 대한 기울기

# 광고비가 1달러 늘어날수록 매출은 평균적으로 2.84달러 증가한다.
# 프로모션 예산이 1달러 늘어날수록 매출은 평균적으로 0.57달러 증가한다.
# 웹사이트 방문자수가 1명 늘어날수록 매출은 평균적으로 1.42달러 증가한다.
# 결정계수값이 0.99이므로 거의 1에 가깝기 때문에 모델이 매출의 변화를 잘 예측하고 있다.
다중회귀분석 예시코드3 - 회귀계수가 음수일 때 해석해보기
import numpy as np
import pandas as pd
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
# 주어진 데이터로 데이터프레임 생성
data = {
"광고비_TV ($)": [10000, 15000, 20000, 25000, 30000, 35000, 40000, 45000, 50000, 55000],
"광고비_온라인 ($)": [5000, 10000, 15000, 20000, 25000, 30000, 35000, 40000, 45000, 50000],
"SNS_언급량 (건)": [200, 400, 800, 1200, 1600, 2000, 2400, 2800, 3200, 3600],
"검색량_브랜드명 (건)": [5000, 7000, 9000, 12000, 15000, 18000, 21000, 24000, 27000, 30000],
"웹사이트 방문자 수 (명)": [8000, 11000, 14000, 18000, 22000, 26000, 30000, 34000, 38000, 42000],
"고객 설문 점수 (100점 만점)": [65, 68, 72, 75, 78, 82, 85, 88, 90, 93],
"SNS 공유 횟수 (회)": [100, 300, 600, 1000, 1500, 2000, 2500, 3000, 3500, 4000],
"인플루언서 협업 수 (건)": [5, 8, 12, 15, 18, 22, 25, 28, 30, 35],
"브랜드 인지도 점수 (100점 만점)": [50, 55, 60, 65, 70, 75, 80, 85, 90, 95]
}
df = pd.DataFrame(data)
# 다중 회귀 분석 수행
X = df.drop(columns=["브랜드 인지도 점수 (100점 만점)"])
y = df["브랜드 인지도 점수 (100점 만점)"]
model = LinearRegression()
model.fit(X, y)
# 예측 결과
predicted_brand_awareness = model.predict(X)
r2 = r2_score(y, predicted_brand_awareness)
# 회귀 계수 출력
광고비_TV_coef = model.coef_[X.columns.get_loc("광고비_TV ($)")]
광고비_온라인_coef = model.coef_[X.columns.get_loc("광고비_온라인 ($)")]
SNS_언급량_coef = model.coef_[X.columns.get_loc("SNS_언급량 (건)")]
검색량_브랜드명_coef = model.coef_[X.columns.get_loc("검색량_브랜드명 (건)")]
웹사이트_방문자_수_coef = model.coef_[X.columns.get_loc("웹사이트 방문자 수 (명)")]
고객_설문_점수_coef = model.coef_[X.columns.get_loc("고객 설문 점수 (100점 만점)")]
SNS_공유_횟수_coef = model.coef_[X.columns.get_loc("SNS 공유 횟수 (회)")]
인플루언서_협업_수_coef = model.coef_[X.columns.get_loc("인플루언서 협업 수 (건)")]
coef_list = [
("광고비_TV ($)", 광고비_TV_coef),
("광고비_온라인 ($)", 광고비_온라인_coef),
("SNS_언급량 (건)", SNS_언급량_coef),
("검색량_브랜드명 (건)", 검색량_브랜드명_coef),
("웹사이트 방문자 수 (명)", 웹사이트_방문자_수_coef),
("고객 설문 점수 (100점 만점)", 고객_설문_점수_coef),
("SNS 공유 횟수 (회)", SNS_공유_횟수_coef),
("인플루언서 협업 수 (건)", 인플루언서_협업_수_coef)
]
# 절대값 기준으로 정렬
sorted_coef_list = sorted(coef_list, key=lambda x: abs(x[1]), reverse=True)
# 가장 영향력이 큰 변수
most_influential_variable = sorted_coef_list[0]
# 최종 결과 출력
final_results = {
"회귀 분석 결정계수 (R²)": r2,
"가장 영향력이 큰 변수": most_influential_variable,
"회귀 계수 목록": sorted_coef_list,
}
final_results
# Q1
# 가장 중요한 변수는 광고비_온라인 인것으로 나타났다.(광고비_TV와 극소한 차)
# 광고비_온라인이 1달러 증가할 때마다 브랜드 인지도 점수는 약 0.000495점 증가한다.
# Q2
# TV 광고와 온라인 광고는 극소한 차이를 보이므로 둘 다 효과적인 광고채널이다. (1위, 2위)
# TV 광고와 온라인 광고 동등하게 예산배분을 하는 것이 좋음.
# Q3
# 인플루언서 협업의 회귀계수 값이 거의 0에 수렴해서 브랜드 인지도 증가에 거의 영향을 주지 않는다고 봄.
# 인플루언서 협업의 중요도는 적은 것으로 보인다.
# 인플루언서 협업의 중요도가 적으므로 브랜드 인지도 점수를 90으로 만들기 위해서는
# 인플루언서 협업보다는 영향력이 큰 다른 변수들에 신경을 쓰는 것이 좋다.
# Q4
# SNS공유 횟수와 SNS 언급량은 브랜드 인지도 증가에 거의 기여를 하지 않는다고 볼 수 있음.(0에 수렴)
# 둘다 브랜드 인지도 증가에 거의 영향을 끼치지 않는다.
# 둘다 부정적, 긍정적 영향 거의 없음
# Q5
# 고객설문점수 80점, 웹사이트 방문자수 30,000명일때 예측된 브랜드 인지도 점수: 1.49
# 고객설문점수가 증가하면 브랜드 인지도 점수는 미미하게 떨어지나 영향이 거의 없다.(0에 가까운 음수)
# 고객설문점수를 85점으로 높이면 브랜드 인지도 점수는 미미하게 떨어짐. (0에 가까운 음수)
※ 다중 회귀분석에서 회귀계수가 음수인 경우, 해당 독립변수가 종속변수에 부정적인 영향을 미친다는 의미.
즉, 그 독립변수가 1단위 증가할 때 종속변수는 그만큼 줄어든다고 해석할 수 있음.
'데이터 분석 part' 카테고리의 다른 글
| 마케팅 데이터의 주요 지표 분석 (보고서 실습) (2) | 2025.02.27 |
|---|---|
| 상관관계의 이해, 상관분석 / 웹시스템 이용한 마케팅 데이터 획득 이해 (0) | 2025.02.25 |
| 통계의 기본개념 (0) | 2025.02.21 |
| EDA (탐색적 데이터 분석) (0) | 2025.02.20 |
| 그로스 마케팅에서의 그래프 사용, 데이터 변환의 중요성 (0) | 2025.02.19 |