고객 세분화를 위한 통계 분석
고객 세분화는 고객의 특성(특징)과 행동패턴을 분석하여 비슷한 그룹으로 나누는 과정이다. → 군집화(clustering)
고객 세분화를 위한 대표적 통계 분석기법으로는 기술 통계 분석, K-평균 군집 분석, RFM 분석, 계층적 군집 분석이 있다.
기술 통계 분석
- 데이터의 분포와 기본적인 특징을 파악하는데 사용 (EDA)
- 평균 (Mean): 고객 1인당 평균 구매 금액, 평균 방문 횟수 등을 분석. 평균은 그 데이터들을 대표하는 값
- 중앙값 (Median): 데이터의 중앙값을 계산하여 이상치의 영향을 최소화
- 표준편차 (Standard Deviation): 고객 간 소비 패턴의 차이 파악, 중심값에서 얼마나 떨어져 있는지.
- 최댓값 및 최솟값 (Max & Min): 가장 높은 구매 금액과 가장 낮은 구매 금액 확인.
예제 코드 ( 주어진 데이터의 대표적인 통계 지표들 알아내기)
# pandas를 pd라는 별칭으로 불러온다.
import pandas as pd
# data 딕셔너리 생성
data = {
"고객ID": range(1, 11),
"총구매금액": [50000, 150000, 30000, 400000, 120000, 80000, 60000, 200000, 90000, 250000],
"방문횟수": [5, 20, 3, 40, 12, 8, 6, 25, 10, 35]
}
# data 딕셔너리를 데이터 프레임 (표)에 담는다.
df = pd.DataFrame(data)
# 기술 통계 분석 수행
# describe() 함수 : pandas 데이터프레임에서 요약 통계 정보를 제공하는 함수(평균, 표준 편차, 최솟값, 최대값 등)
summary_stats = df.describe()
# 통계 요약정보 출력 (보기쉽게 display)
display(summary_stats)
- count > 데이터 개수
- mean > 평균 (모든 값의 합을 데이터 개수로 나눈 값)
- std > 표준 편차 ( 값들이 평균에서 얼마나 떨어져 있는지 )
- min > 최솟값 (가장 작은 값)
- 25%(1사분위,Q1) > 하위 25% 지점의 값
- 50% (2사분위, 중앙값, Median, Q2) > 중앙값 (전체 데이터의 정중앙 값, 평균과 다를 수 있음)
- 75% (3사분위, Q3) > 상위 75% 지점의 값
- max > 최댓값 (가장 큰 값)
K-평균 군집 분석 (K-Means Clustering)
- 현업에서 99% 이것을 쓴다.
- 주어진 데이터를 K개의 군집(cluster)으로 나누는 비교사 학습 알고리즘 (label이 없음)
- 각 데이터 포인트가 가장 가까운 중심(centroid)에 속하도록 반복적으로 업데이트하는 방식
- 데이터를 비슷한 속성을 가진 그룹으로 묶을 때 유용.
- 고객을 여러 개의 그룹으로 나누는 방법. 유사한 특성을 가진 고객끼리 묶어 그룹을 생성
- 그룹의 개수(K)는 사전에 지정해야 한다. ( 으로 설정하면, 고객을 3개의 그룹으로 나눌 수 있음)
- 이 방법을 사용하면 고객을 고가 제품 선호 그룹, 할인 제품 선호 그룹 등으로 구분할 수 있다.

# K- 평균 군집 알고리즘 과정
- 초기 중심(K 개의 중심 선택)
- 무작위로 K개의 중심을 설정.
- 각 데이터 포인트를 가장 가까운 중심에 할당
- 유클리드 거리(보통 사용)를 기준으로 가장 가까운 중심에 각 데이터를 배정.
- 새로운 중심 계산
- 각 군집에 속한 데이터들의 평균을 구해서 새로운 중심을 업데이트 함.
- 수렴할 때까지 반복
- 중심이 더 이상 변하지 않거나, 특정 조건(반복 횟수 제한 등)이 충족될 때까지 2~3단계를 반복.
# K-평균 군집의 장단점
- 장점
- 단순하고 빠르게 동작함 (큰 데이터에도 적용 가능)
- 해석이 직관적임
- 비교적 계산 비용이 낮음
- 단점
- 군집 개수 K를 미리 정해야 함 → K값을 잘못 설정하면 의미 없는 군집이 만들어질 수도 있음.
- 이상치(outlier)에 민감함 → 값이 극단적으로 크거나 작은 데이터가 있으면 군집이 잘못 형성될 수도 있음.
- 원형(구형) 형태의 군집에 적합하지만, 복잡한 모양의 군집을 찾기 어려움
- 단점 보완 방법
- 이상치를 미리 제거하거나 DBSCAN 같은 밀도 기반 군집 알고리즘을 사용할 수도 있음.
- K값을 정할 때 엘보우 기법을 사용하거나 실루엣 분석(Silhouette Score)을 활용할 수 있음.
예제 코드
import matplotlib.pyplot as plt # 그래프 그릴 때
from sklearn.cluster import KMeans # K-평균 군집 수행 도구
import pandas as pd # 데이터프레임 생성해야하니까 pandas도 필요
import koreanize_matplotlib # 그래프에 한글 안깨지려면 꼭
# data라는 딕셔너리 생성
data = {
"고객ID": range(1, 11), # 고객 1번~10번까지 고객 ID
"총구매금액": [50000, 150000, 30000, 400000, 120000, 80000, 60000, 200000, 90000, 250000],
"방문횟수": [5, 20, 3, 40, 12, 8, 6, 25, 10, 35]
}
# data를 pandas 데이터프레임(표)에 담음
df = pd.DataFrame(data)
# X만 있고 Y는 없다. 이유는 K-means는 비교사학습이기 때문에
# 클러스터링에 사용할 특성 선택 (총 구매금액, 방문 횟수)
X = df[["총구매금액", "방문횟수"]]
# K-Means 클러스터링 수행
# KMeans() : K평균 군집분석 수행
# n_cluster = K개수(분류개수)(3개로설정) / random-state : 랜덤성을 고정하는 숫자(42는 그냥 관례) - 이거 안하면 실행할 때마다 결과가 달라질 수 있어서 이걸로 고정해야함.
# fit_predict(X) → 데이터를 학습해서 각 데이터가 어느 군집에 속하는지 예측.
# df["군집"] = ... → 군집 정보를 df에 새로운 열로 추가.
kmeans = KMeans(n_clusters=3, random_state=42)
df["군집"] = kmeans.fit_predict(X)
# 시각화
plt.scatter(X["총구매금액"], X["방문횟수"], c=df["군집"], cmap="viridis", alpha=0.7)
plt.xlabel("총 구매 금액")
plt.ylabel("방문 횟수")
plt.title("K-Means 군집 분석 결과")
plt.colorbar()
plt.show()
- X축 (총 구매 금액)
- 고객이 지출한 총 금액
- 오른쪽으로 갈수록 많이 구매한 고객
- Y축 (방문 횟수)
- 해당 고객이 방문한 횟수
- 위로 갈수록 자주 방문한 고객
- 색깔 (군집 그룹)
- 같은 색상끼리 묶여 있는 점들은 같은 군집으로 분류됨.
- 색상은 우측 컬러바(0, 1, 2 등)로 표시된 군집 ID를 의미.
결과 해석
- 아래쪽 왼쪽 (청록색 군집)
- 방문 횟수도 적고, 구매 금액도 낮은 고객들.
- 일반적인 소액 구매 고객군으로 보임.
- 중간 (노란색 군집)
- 방문 횟수도 많고, 구매 금액도 높은 고객들.
- 충성도가 높은 우수 고객군일 가능성이 높음.
- 오른쪽 위 (보라색 군집, 혹은 이상치?)
- 방문 횟수와 구매 금액이 유독 높은 고객.
- VIP 고객이거나 특이한 구매 패턴을 가진 고객일 수도 있음.
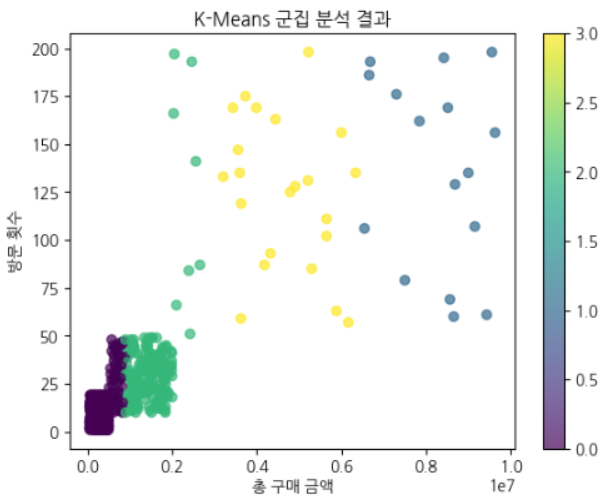
K=4 로 변경하였더니 소액 구매고객이 2분류로 더 나뉘었음.
소액 자주 방문 고객, 소액 가끔 방문 고객으로 구분되었음.
RFM 분석
- 현업에서 잘 안씀.
- 고객을 최근성(Recency), 빈도(Frequency), 금액(Monetary) 기준으로 평가하여 고객의 가치를 측정하는 방법
( 부모님이 자식 평가기준, 썸탈 때 썸남평가로 비유 ㅎ)
- 최근성 (Recency): 고객이 마지막으로 구매한 날짜를 기준으로 측정
- 빈도 (Frequency): 일정 기간 동안 고객이 구매한 횟수를 측정
- 금액 (Monetary): 고객이 사용한 총 금액을 기준으로 평가
이 분석을 통해 VIP 고객, 일반 고객, 이탈 가능 고객을 구분할 수 있다.
예제코드
import numpy as np
# 고객 10명의 데이터 생성
# 구매일은 2024-01-01부터 30일 간격으로 10개 생성
# 총구매금액은 각 고객이 소비한 금액
data = {
"고객ID": range(1, 11),
"구매일": pd.date_range(start="2024-01-01", periods=10, freq="30D"),
"총구매금액": [50000, 150000, 30000, 400000, 120000, 80000, 60000, 200000, 90000, 250000]
}
# pandas 데이터프레임에 담기
df = pd.DataFrame(data)
# 현재 날짜 기준 최근성 계산
# 오늘 날짜에서 구매일을 뺀 값 → 얼마나 오래 전에 구매했는지 계산
# 값이 작을수록 최근에 구매한 고객
df["Recency"] = (pd.to_datetime("today") - df["구매일"]).dt.days
# 빈도와 금액 계산
# Frequency는 1~20 사이 랜덤 값 → 고객이 몇 번 구매했는지
# Monetary는 총구매금액과 동일
df["Frequency"] = np.random.randint(1, 20, len(df))
df["Monetary"] = df["총구매금액"]
# RFM 점수 부여
# pd.qcut()을 사용하여 5개의 그룹으로 나눔
# R_Score: Recency가 낮을수록 점수 높음 (최근 구매한 고객이 높은 점수)
# F_Score: Frequency가 높을수록 점수 높음 (자주 구매한 고객이 높은 점수)
# M_Score: Monetary가 높을수록 점수 높음 (많이 소비한 고객이 높은 점수)
df["R_Score"] = pd.qcut(df["Recency"], 5, labels=[5, 4, 3, 2, 1])
df["F_Score"] = pd.qcut(df["Frequency"], 5, labels=[1, 2, 3, 4, 5])
df["M_Score"] = pd.qcut(df["Monetary"], 5, labels=[1, 2, 3, 4, 5])
# RFM_Score = R + F + M
# 총점이 높을수록 우수 고객
df["RFM_Score"] = df["R_Score"].astype(int) + df["F_Score"].astype(int) + df["M_Score"].astype(int)
# 고객별로 Recency, Frequency, Monetary, RFM_Score 값을 출력
print(df[["고객ID", "Recency", "Frequency", "Monetary", "RFM_Score"]])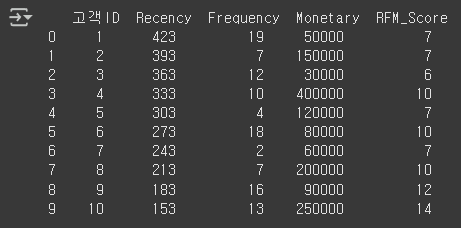
계층적 군집 분석 (dendrogram)
- 현업에서 거의 안씀.
- 고객을 계층 구조로 그룹화하여 유사도에 따라 점진적으로 병합하는 방법.
- 이 분석을 통해 고객을 세부적인 등급으로 나눌 수 있다.
예제 코드
from scipy.cluster.hierarchy import linkage, dendrogram
# 10명의 고객 데이터 생성
data = {
"고객ID": range(1, 11),
"총구매금액": [50000, 150000, 30000, 400000, 120000, 80000, 60000, 200000, 90000, 250000],
"방문횟수": [5, 20, 3, 40, 12, 8, 6, 25, 10, 35]
}
# 데이터 프레임에 담기
df = pd.DataFrame(data)
# 총구매금액, 방문횟수 → 군집 분석에 사용할 변수 선택
X = df[["총구매금액", "방문횟수"]]
# 계층적 군집 분석 수행
# linkage() 함수: 군집을 계층적으로 묶는 함수
# method="ward": 군집 내 데이터 간의 분산(Variance)을 최소화하는 방법, 거리 기반이 아니라 데이터 내 변동성을 최소화하도록 군집을 형성
linkage_matrix = linkage(X, method="ward")
# 덴드로그램 시각화
# dendrogram() 함수: 덴드로그램 그리기
plt.figure(figsize=(10, 5))
dendrogram(linkage_matrix)
plt.title("계층적 군집 분석 (Dendrogram)")
plt.xlabel("고객 인덱스")
plt.ylabel("거리")
plt.show()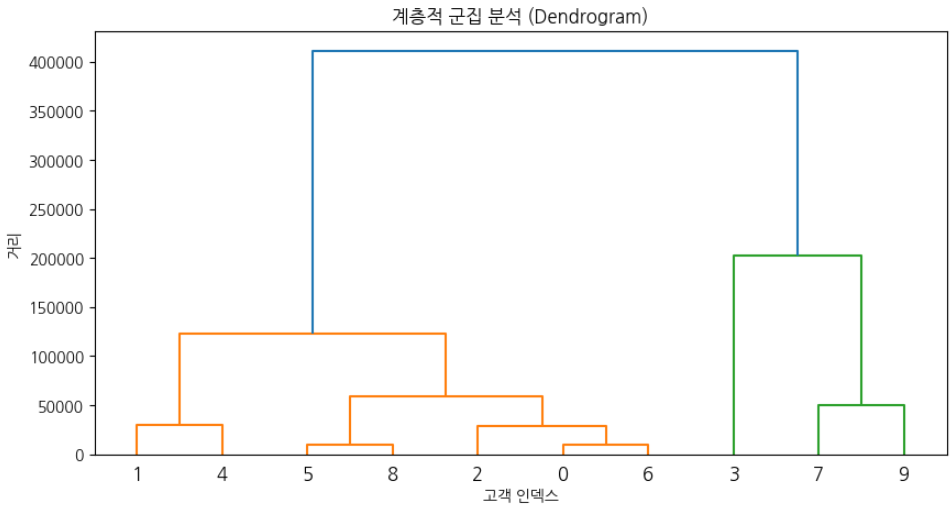
- 아래쪽에서 위쪽으로 갈수록 군집이 합쳐짐
- Y축(거리)이 클수록 군집 간 차이가 크다는 의미
- 특정 높이에서 가지를 끊으면 군집 개수를 조절 가능
기술 통계 분석 → 고객의 기본적인 특성을 이해
K-평균 군집 분석 → 고객을 명확한 그룹으로 나누어 맞춤형 마케팅 진행 가능
RFM 분석 → VIP 고객과 일반 고객을 구별하여 적절한 마케팅 전략 적용
계층적 군집 분석 → 고객의 특성을 더욱 세부적으로 분석
확률변수
- 불확실한 사건의 결과를 수치화하는 변수
- 이산형 확률변수와 연속형 확률변수로 나뉜다.
※ 각 분포가 무작위성을 포함하고 있으므로, 실행할 때마다 값이 달라질 수 있다.
이산 확률변수 (Discrete Random Variable)
- 특정한 개별 값만 가질 수 있는 확률변수
- ex) 동전 던지기(앞면=1, 뒷면=0), 주사위 눈금(1,2,3,4,5,6), 고객의 구매 횟수(정수값)
- 대표적인 이산 확률 분포 : 베르누이 분포, 이항 분포, 포아송 분포
# 베르누이 분포
# 확률 분포 그래프
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from scipy.stats import bernoulli, binom, poisson, norm, expon, gamma, beta
# 데이터 시드 설정
np.random.seed(42)
# 1. 베르누이 분포 (Bernoulli Distribution) - 광고 클릭 여부 (0 or 1)
bernoulli_data = bernoulli.rvs(p=0.3, size=1000)
plt.figure(figsize=(8, 5))
sns.histplot(bernoulli_data, discrete=True, kde=False, bins=2)
plt.xlabel("광고 클릭 여부 (0: 실패, 1: 성공)")
plt.ylabel("빈도")
plt.title("베르누이 분포 (Bernoulli Distribution)")
plt.xticks([0, 1])
plt.grid()
plt.show()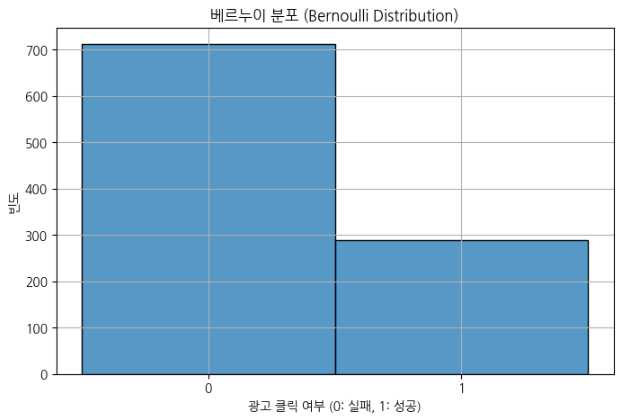
- 단일 시행(즉, 한 번의 실험)에서 성공(1) 또는 실패(0) 중 하나의 값을 가지는 확률모델
- 특정 사건이 발생할 확률을 나타냄 (예: 광고 클릭 여부, 0 또는 1)
# 이항 분포
# 2. 이항 분포 (Binomial Distribution) - 10번 광고 노출 중 클릭 횟수
binom_data = binom.rvs(n=10, p=0.3, size=1000)
plt.figure(figsize=(8, 5))
sns.histplot(binom_data, discrete=True, kde=False, bins=11)
plt.xlabel("클릭 횟수")
plt.ylabel("빈도")
plt.title("이항 분포 (Binomial Distribution)")
plt.grid()
plt.show()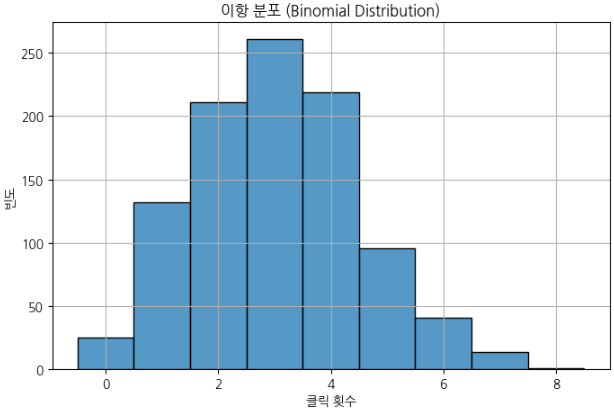
- 여러 번 시행 중 성공이 나오는 횟수 분포 (0부터 n까지의 값)
- 일정 횟수(n) 동안 특정 사건이 발생하는 횟수를 모델링 (예: 10번의 광고 노출 중 클릭 횟수)
- 베르누이 분포는 이항 분포의 특수한 경우. 즉, 이항 분포에서 시행 횟수 n=1이면 베르누이 분포가 됨.
※ 베르누이 분포와 이항 분포의 차이
동전을 10번 던졌을 때 앞면이 나온 횟수를 생각했을 때,
- 각 동전 던지기는 베르누이 시행임. (앞면: 1, 뒷면: 0)
- 근데 이걸 10번 반복하면, 앞면이 나오는 총 횟수가 0부터 10까지 나올 수 있음.
- 즉, 이항 분포에서는 확률 변수 X가 0부터 n까지의 정수 값 (성공횟수)을 가질 수 있음.
| 구분 | 베르누이 분포 | 이항 분포 |
| 실험 횟수 | 단 한 번의 시행 (n=1) | 여러 번의 시행 (n≥1) |
| 확률 변수 (X) 값 | 0 또는 1 (성공 or 실패) | 0부터 n까지 (성공 횟수) |
| 의미 | 한 번의 성공/실패 여부 | 여러 번 시행했을 때 성공한 횟수 |
# 포아송 분포
- 마케팅에서 중요 (ex. 오프라인 매장에서 매장관리, 접속률이 늘어나는 시간대에 이벤트)
# 3. 포아송 분포 (Poisson Distribution) - 1시간 동안 유입되는 고객 수
poisson_data = poisson.rvs(mu=5, size=1000)
plt.figure(figsize=(8, 5))
sns.histplot(poisson_data, discrete=True, kde=False, bins=15)
plt.xlabel("1시간 동안 유입된 고객 수")
plt.ylabel("빈도")
plt.title("포아송 분포 (Poisson Distribution)")
plt.grid()
plt.show()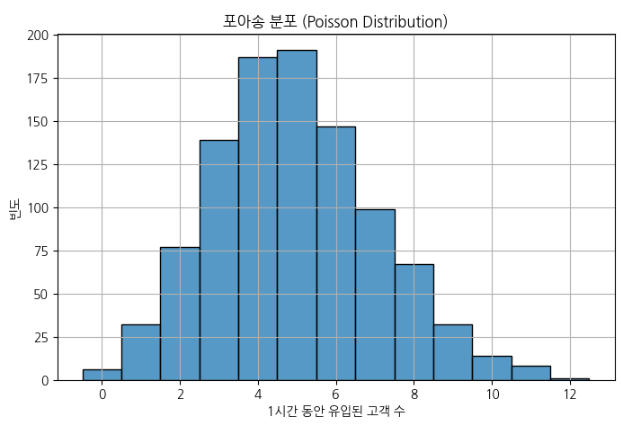
- 일정 시간 내에 발생하는 이벤트 횟수 분포
- 단위 시간당 발생하는 이벤트 수를 모델링 (예: 1시간 동안 유입된 고객 수)
※ 포아송 분포(Poisson Distribution)의 특징
- 일정한 시간 또는 공간에서 어떤 사건이 발생하는 횟수를 나타내는 확률 분포
- 1시간 동안 들어오는 고객 수, 웹사이트 방문 횟수, 콜센터의 전화 수 등
1. 정의
포아송 분포는 평균 발생 횟수(λ, 람다)가 주어졌을 때 특정 개수의 사건이 발생할 확률을 나타내는 분포.
확률 질량 함수 (PMF) :
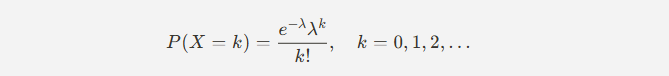
- (람다): 일정한 시간이나 공간에서 사건이 발생하는 평균 횟수 (기대값 = 평균)
- X : 일정 시간 또는 공간 내에서 발생하는 사건의 횟수
- k: 사건이 발생한 횟수 (0, 1, 2, …)
- e : 자연상수 (약 2.718)
- X는 포아송 분포를 따르는 확률 변수. 특정한 시간이나 공간에서 발생하는 사건의 개수를 나타내는 변수. 예를 들어 '1시간 동안 들어오는 고객수'가 X라고 할 수 있음.
- k는 확률변수 X가 가질 수 있는 구체적인 값. 예를 들어 '1시간 동안 고객이 정확히 7명 올 확률'을 구하고 싶다면, 여기서 K=7이 되는 것임. 즉, X가 특정한 값 k를 가질 확률을 구할 때 쓰는 것.
- 포아송 분포에서 기대값(평균)과 분산이 모두 . 즉, 가 크면 사건이 자주 발생하고, 작으면 드물게 발생하는 것.
예제)
카페에 1시간 동안 평균 5명의 손님이 온다고 하면 λ=5.
이때, 1시간 동안 정확히 7명이 올 확률을 구할 때, λ=5를 사용.
: "1시간 동안 카페에 오는 손님 수" (확률 변수)
k: X가 가질 수 있는 값 (0, 1, 2, 3, ...)
이제 만약 "정확히 7명이 올 확률" 을 알고 싶다면?
이때 X=7일 확률을 구하는 것임.
즉, P(X=7)을 계산하는 것.
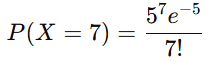
2. 포아송 분포의 특징
1) 이산 확률 분포
- 포아송 분포는 이산형 확률 분포로, 사건 발생 횟수가 0, 1, 2, 3과 같은 정수값을 가짐.
2) 평균과 분산이 동일
- 포아송 분포의 평균과 분산은 동일하며, 둘 다 λ이다.
- 평균 (기대값) : E(X) = λ
- 분산 : Var(X) = λ
- 따라서 λ 값이 클수록 데이터의 퍼짐도(변동성)가 증가한다.

3) 사건 발생이 독립적
- 서로 다른 시간대 또는 공간에서 발생한 사건들은 독립적이다.
- 예: 오후 1시의 고객 유입 수는 오후 2시의 고객 유입 수와 관계없이 발생한다고 가정.
4) 희귀 이벤트 모델링에 적합
- 이벤트가 드물게(rare) 발생하는 경우를 모델링하는 데 유용.
- 예: 특정 질병이 하루에 몇 명에게 발병하는가?
- 예: 공장에서 특정 결함이 발생하는 횟수
5) 단위 시간 또는 공간이 증가하면 정규 분포에 수렴
- λ 값이 커지면 포아송 분포는 정규 분포에 근사한다.
- 중심극한정리(CLT)에 의해 큰 λ에서는 정규 분포와 유사한 형태를 가짐.
6) 포아송 과정 (Poisson Process)
- 포아송 분포는 보통 시간(또는 공간)에 따라 랜덤하게 발생하는 이벤트를 모델링할 때 사용되며, 이 과정은 포아송 과정(Poisson Process)이라 부름.
- 포아송 과정은 특정 단위 시간 내에서 사건이 발생할 확률이 일정하고, 각 사건이 독립적으로 발생하는 경우 적용됨.
3. 포아송 분포 적용 사례
1) 웹사이트 방문 분석
- 시간당 방문자 수를 모델링 하여 트래픽 변화를 분석
2) 고객 유입 예측
- 매장에서 1시간 동안 도착하는 고객 수 예측 (그로스 마케팅 활용)
# 포아송 분포를 따르는 난수(고객수) 생성을 위해 numpy 라이브러리 불러옴.
import numpy as np
# 설정: 매장 시간당 평균 고객 유입 수 (λ)
lambda_value = 7 # 시간당 평균 7명의 고객 방문
# 1시간 동안 도착하는 고객 수 예측 (포아송 분포 샘플링)
# np.random.poisson(λ) : 포아송 분포를 따르는 난수를 생성하는 함수
# 즉, "1시간 동안 몇 명의 고객이 올지" 랜덤하게 예측하는 역할
predicted_customers = np.random.poisson(lambda_value)
# 결과 출력 (실행할 때마다 값이 달라짐)
print(f"예측된 1시간 동안 도착하는 고객 수: {predicted_customers}")
실행할 때마다 결과가 다르게 나오는 이유는 포아송 분포에서 난수를 생성하기 때문이다.
컴퓨터는 np.random.poisson(λ) 을 실행할 때 완전히 일정한 값이 아니라, 확률적으로 변화하는 값을 생성.
포아송 분포에서 λ (평균 발생 횟수) 를 중심으로 랜덤하게 숫자를 뽑기 때문.
포아송 분포는 "평균적으로 λ 만큼 발생한다"는 성질을 가지고 있지만,
항상 딱 λ 값이 나오는 게 아니라, 그 주변에서 랜덤하게 값이 나온다.
즉, 결과는 확률적으로 변하지만, 평균적으로 7에 가까운 값이 나온다.
np.random.poisson(λ) 는 내부적으로 의사난수를 생성.
진짜 랜덤이 아니라, 알고리즘을 사용해서 난수를 만듦.
실행할 때마다 같은 결과를 얻고 싶다면,
난수를 생성할 때 랜덤 시드(seed)를 고정하면, 실행할 때마다 같은 결과를 얻을 수 있음.
→ np.random.seed(42)
- np.random.poisson(λ) 는 포아송 분포를 따르는 난수를 생성
평균 λ 를 기준으로 값이 랜덤하게 변함
항상 같은 값이 나오지 않는 이유는 확률적으로 변하는 값이기 때문
같은 결과를 얻고 싶다면 np.random.seed(42) 를 사용하면 됨
- 여러 시간대를 예측할 수도 있음. (예 : 10시간 동안의 고객 유입)
# 여러 시간대 예측 (예: 10시간 동안의 고객 유입 수) - 이전 코드에 이어서..
# np.random.poisson(lambda_value, hours) : 포아송 분포를 따르는 난수를 10개 생성. 각 값은 1시간 동안의 예상 고객 수
# hours 변수 값이 10으로 설정되어 있기 때문에 10개의 난수를 생성.
# 첫 번째 인수 lambda_value는 평균 발생 횟수 (여기서는 7)
# 두 번째 인수 hours는 생성할 난수의 개수로, hours = 10 이기 때문에 10개를 생성하도록 지정.
hours = 10 # 10시간 동안의 고객 유입을 예측
predicted_customers_per_hour = np.random.poisson(lambda_value, hours)
# 예측 결과 출력 (실행할 때마다 값이 다를 수 있음)
# .min() → 배열에서 가장 작은 값 찾기
# .max() → 배열에서 가장 큰 값 찾기
# .mean() → 10시간 동안의 평균 고객 수 계산
# :.2f → 소수점 둘째 자리까지 출력
print(f"각 시간대별 예측된 고객 수: {predicted_customers_per_hour}")
print(f"최소 고객 수: {predicted_customers_per_hour.min()}, 최대 고객 수: {predicted_customers_per_hour.max()}")
print(f"평균 고객 수: {predicted_customers_per_hour.mean():.2f}")
각 숫자는 1시간 동안의 예상 고객 수를 나타냄.
첫 번째 숫자 9은 첫 번째 시간에 고객이 9명 방문할 것으로 예측된다는 의미.
np.random.poisson(λ, size) : λ는 평균 발생횟수, size는 생성할 난수 개수
- 평균적으로 λ 값에 가까운 값들이 나옴
- 하지만 매번 결과가 같진 않음 (난수 생성)
- 포아송 분포는 확률 분포이기 때문에 평균적으로 λ 에 가까운 값이 나오지만, 랜덤하게 변동 가능
- np.random.seed(42) 를 설정하면 항상 같은 결과를 얻을 수 있음
3) 콜센터 전화량 분석
- 시간당 들어오는 콜센터 전화 수 예측
4) 결함 검출
- 공장에서 시간당 발생하는 결함 제품 수 분석
5) 교통사고 발생 분석
- 특정 도로에서 하루 동안 발생하는 사고 횟수 분석
4. 포아송 분포 vs 다른 분포 비교
| 분포 | 특징 | 주요 차이점 |
| 이항 분포 | 고정된 시행 횟수 n과 성공 확률 p가 있을 때 성공 횟수를 모델링 | 포아송 분포는 무한한 시행 가능성을 가정 (이항 분포는 고정된 n) |
| 정규 분포 | 연속 확률 분포로 평균과 표준편차를 기반으로 확률 계산 | 포아송 분포는 이산 분포, λ가 크면 정규 분포에 수렴 |
| 지수 분포 | 사건이 발생하는 시간 간격을 모델링 | 포아송 분포는 시간 단위당 이벤트 개수를 모델링 |
포아송 분포를 이용해서 하루 동안의 시간별 고객 유입수를 예측하고 시각화
import numpy as np # 포아송 분포 생성에 사용
import matplotlib.pyplot as plt # 그래프로 시각화할 때
import pandas as pd # 데이터 처리및 분석 (dataframe객체 사용)
# 포아송 분포를 따르는 하루 동안의 고객 유입 데이터 생성 (λ = 평균 유입 고객 수)
lambda_value = 5 # 시간당 평균 5명의 고객이 유입됨
hours = 24 # 하루 24시간. 24시간동안 고객 유입수 예측
# 각 시간대의 고객 유입 수를 포아송 분포에서 샘플링
# np.random.poisson(lambda_value, hours) : 'lambda_value = 5'를 기반으로 24시간 동안 각각의 시간대에 고객이 얼마나 유입될지를 무작위로 생성하는 코드.
customer_arrivals = np.random.poisson(lambda_value, hours)
# 데이터프레임 생성
# Hour: 하루 24시간을 나타내는 0부터 23까지의 시간.
# Customers: 각 시간대에 도착한 고객 수.
df = pd.DataFrame({
'Hour': np.arange(hours),
'Customers': customer_arrivals
})
# 결과 출력
# 각 시간대별 고객 유입 수를 확인
print(df)
# 시각화: 시간별 고객 유입 수
plt.figure(figsize=(10, 5))
plt.bar(df['Hour'], df['Customers'], color='royalblue', alpha=0.7)
plt.xlabel('Hour of the Day')
plt.ylabel('Number of Customers')
plt.title('Hourly Customer Arrivals (Poisson Distribution)')
plt.xticks(np.arange(0, 24, 2))
plt.grid(axis='y', linestyle='--', alpha=0.7)
plt.show()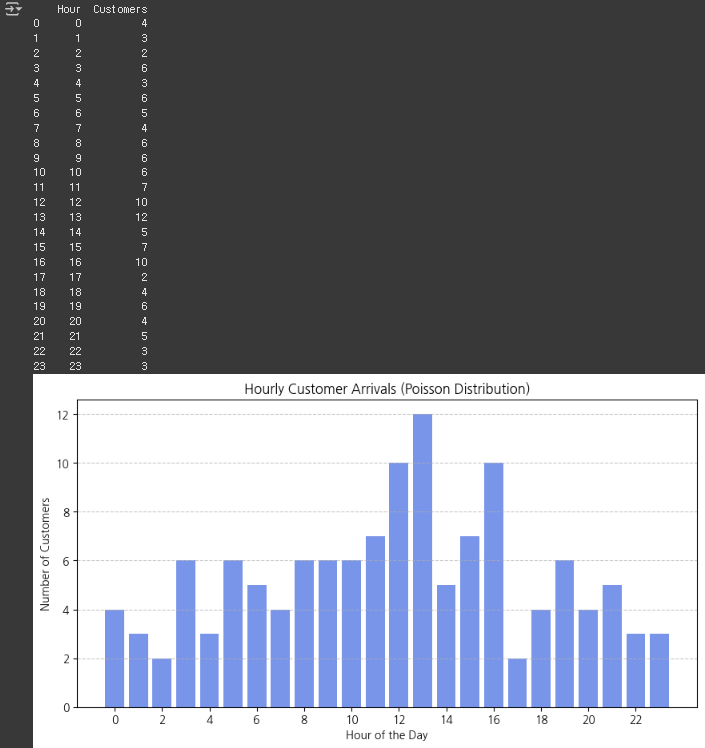
- λ(평균) 값 근처로 분포한다.
- 랜덤성 때문에 실제 결과는 예상보다 적거나 많을 수 있다.
- 여러 번 시뮬레이션을 하면 결과가 평균값 근처에 가까워진다.
연속 확률변수 (Continuous Random Variable)
- 특정 구간 내의 모든 실수 값을 가질 수 있는 확률변수
- 예) 고객의 방문 시간(2.5초, 3.7초 등), 평균 구매 금액(75,000원)
- 대표적인 연속 확률 분포 : 정규 분포, 지수 분포, 감마 분포
# 정규 분포
- 자주 쓰임
# 4. 정규 분포 (Normal Distribution) - 고객 평균 구매 금액
# norm.rvs: scipy.stats.norm 모듈의 rvs(random variates) 함수로, 정규 분포를 따르는 랜덤 샘플을 생성.
# loc=50000: 평균을 50,000원으로 설정. 이 값은 정규 분포의 중심이 되는 값, 즉 고객의 평균 구매 금액.
# scale=15000: 표준편차를 15,000원으로 설정. 표준편차는 데이터가 평균을 중심으로 얼마나 퍼져있는지를 나타냄. 표준편차가 클수록 값들이 더 넓게 퍼지고, 작을수록 값들이 평균에 더 가까워짐.
# size=1000: 1000개의 샘플을 생성하겠다는 의미. 즉, 1000명의 고객이 구매한 금액을 시뮬레이션한다는 것.
norm_data = norm.rvs(loc=50000, scale=15000, size=1000)
# 히스토그램 및 커널 밀도 추정 (KDE) 시각화
# plt.figure(figsize=(8, 5)): 시각화의 크기를 설정. 가로 8, 세로 5 크기의 그래프가 생성.
# sns.histplot: 히스토그램을 그리는 함수
# norm_data: 앞서 생성한 정규 분포 데이터
# kde=True: 커널 밀도 추정(KDE)을 추가로 그리겠다는 옵션. KDE는 데이터를 부드럽게 나타내는 확률 밀도 함수를 추정하는 방법. 즉, 히스토그램의 각 막대가 아닌, 연속적으로 부드럽게 변하는 분포 곡선을 그리게 됨.
# bins=30: 히스토그램을 그릴 때 데이터의 구간을 30개로 나눈다는 의미
plt.figure(figsize=(8, 5))
sns.histplot(norm_data, kde=True, bins=30)
# 시각화 설정
plt.xlabel("구매 금액 (원)")
plt.ylabel("빈도")
plt.title("정규 분포 (Normal Distribution)")
plt.grid()
plt.show()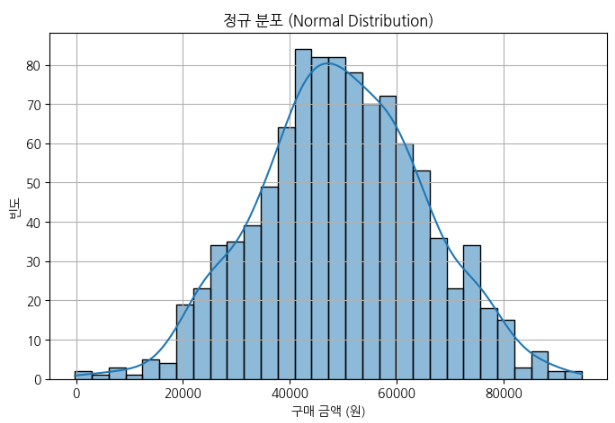
- 자연에서 가장 많이 나타나는 분포, 평균을 중심으로 대칭적인 형태
- 평균, 중앙값, 최빈값이 모두 동일하고, 그래프의 중앙에 위치.
- 정규 분포의 그래프는 종 모양으로 생김. 중앙에서 가장 높은 값을 가지며, 양쪽으로 갈수록 값이 낮아짐.
- (예: 고객 평균 금액)
- 중심 경향성과 퍼짐 정도를 파악하는 데 매우 유용하게 사용
# 지수 분포
- 자주 안씀
# 5. 지수 분포 (Exponential Distribution) - 고객의 체류 시간
# scale=5는 지수 분포의 평균값을 5로 설정. scale 파라미터는 평균 시간을 결정하고, 이는 체류 시간을 설정하는 데 사용. 즉, 평균적으로 고객은 5분 정도 체류할 확률이 높음.
# size=1000은 1000개의 랜덤 샘플을 생성. 즉, 고객의 체류 시간이 1000번 샘플링되어 생성
expon_data = expon.rvs(scale=5, size=1000)
# kde=True는 확률 밀도 함수 (KDE)를 추가하여 데이터의 분포를 부드럽게 표현하는 옵션
# bins=30은 히스토그램의 구간을 30개로 나누는 것.
plt.figure(figsize=(8, 5))
sns.histplot(expon_data, kde=True, bins=30)
plt.xlabel("고객 체류 시간 (분)")
plt.ylabel("빈도")
plt.title("지수 분포 (Exponential Distribution)")
plt.grid()
plt.show()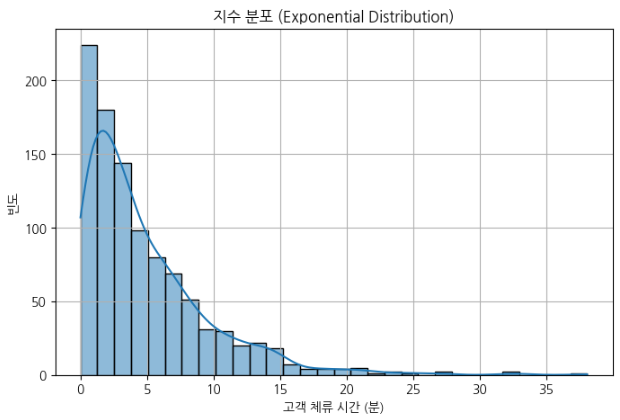
- 사건이 발생하는 시간 간격의 확률 모델
- 대기 시간이나 체류 시간처럼 어떤 일이 발생하기까지 걸리는 시간과 관련된 데이터를 모델링 (예: 고객 체류 시간)
- 평균 (scale): 지수 분포에서 중요한 파라미터는 scale로, 이는 평균값과 동일함. 예를 들어 scale=5이면, 고객의 평균 체류 시간이 5분 정도라고 볼 수 있음.
- 무기억성 (Memoryless): 지수 분포는 "무기억성"을 가지고 있다. 즉, 특정 시간이 경과했다고 해서 앞으로 얼마나 더 시간이 걸릴지에 대한 예측에 영향을 미치지 않는다는 특성이 있음.
- 모양: 지수 분포는 한쪽으로 기울어진 분포를 가지며, 시간의 흐름에 따라 빈도가 급격히 감소하는 형태를 띈다. 즉, 대체로 짧은 시간에 체류하는 경우가 많고, 시간이 길어질수록 체류하는 고객이 적어짐.
# 감마 분포
- 자주 안씀
# 6. 감마 분포 (Gamma Distribution) - 고객 생애 구매 횟수
# a=2 → 형상 모수 (shape parameter, k): 감마 분포의 모양을 결정하는 값. 값이 클수록 분포가 오른쪽으로 퍼지고, 값이 작을수록 지수 분포처럼 한쪽으로 기울어진 모양을 띈다.
# scale=2 → 척도 모수 (scale parameter, θ): 데이터의 평균과 분산을 조절하는 값. 보통 감마 분포의 기대값(평균)은 k×θ로 계산됨.
# size=1000 → 1000개의 랜덤 샘플을 생성. 즉, 1000명의 고객이 평생 몇 번 구매할지를 시뮬레이션한다고 보면 됨.
gamma_data = gamma.rvs(a=2, scale=2, size=1000)
# kde=True는 확률 밀도 함수 (KDE)를 함께 그려서 분포를 부드럽게 표현하는 옵션.
# bins=30 → 히스토그램의 구간 개수를 30개로 설정해서 좀 더 세밀한 분포를 확인.
plt.figure(figsize=(8, 5))
sns.histplot(gamma_data, kde=True, bins=30)
plt.xlabel("고객 생애 구매 횟수")
plt.ylabel("빈도")
plt.title("감마 분포 (Gamma Distribution)")
plt.grid()
plt.show()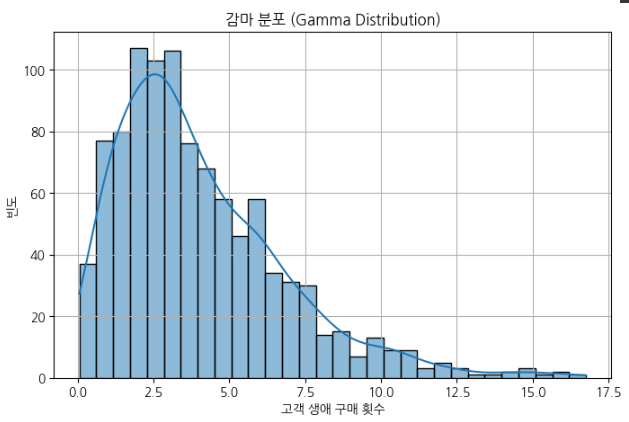
- 여러 개의 지수 분포를 합친 형태
- 고객 생애 구매 횟수 분석에 활용

즉, 고객이 평생 평균적으로 4번 구매할 가능성이 높다고 해석.
감마 분포는 양수만을 가지는 연속 확률 분포. 대기 시간의 합을 모델링할 때 자주 사용.
1) 포아송 과정 (Poisson Process)과 관련됨.
- 감마 분포는 포아송 과정에서 특정 횟수의 이벤트가 발생하는 총 시간을 모델링하는 데 사용.
- 예를 들어, 고객이 평균적으로 한 달에 2번 구매한다고 하면, 고객이 n번 구매하는 데 걸리는 총 시간을 감마 분포로 모델링할 수 있음.
2) 지수 분포의 확장판
- 감마 분포는 지수 분포의 확장 버전.
- 지수 분포는 "첫 번째 구매까지 걸리는 시간"을 모델링하고, 감마 분포는 "n번째 구매까지 걸리는 총 시간"을 모델링.
3) 모양이 다양함
- 감마 분포는 형상 모수 (shape parameter, k)와 척도 모수 (scale parameter, θ)에 따라 다양한 모양을 가질 수 있음.
- k=1일 때는 지수 분포와 동일해지고, k값이 커질수록 정규 분포처럼 점점 대칭적인 형태가 됨.
# 베타 분포
- 자주 안씀
- 전환율 예측하는데 쓰이지만 다른 방법도 많음.
# 7. 베타 분포 (Beta Distribution) - 전환율 예측
# a=2 → 형상 모수(Shape parameter, α): 분포의 모양을 결정하는 첫 번째 값.
# b=5 → 형상 모수(Shape parameter, β): 분포의 모양을 결정하는 두 번째 값.
# size=1000 → 1000개의 랜덤 샘플을 생성. 즉, 1000번의 전환율 샘플링을 의미.
beta_data = beta.rvs(a=2, b=5, size=1000)
# kde=True → 확률 밀도 함수를 추가하여 분포를 부드럽게 표현.
# bins=30 → 30개의 구간으로 나누어 히스토그램을 표현.
plt.figure(figsize=(8, 5))
sns.histplot(beta_data, kde=True, bins=30)
plt.xlabel("전환율")
plt.ylabel("빈도")
plt.title("베타 분포 (Beta Distribution)")
plt.grid()
plt.show()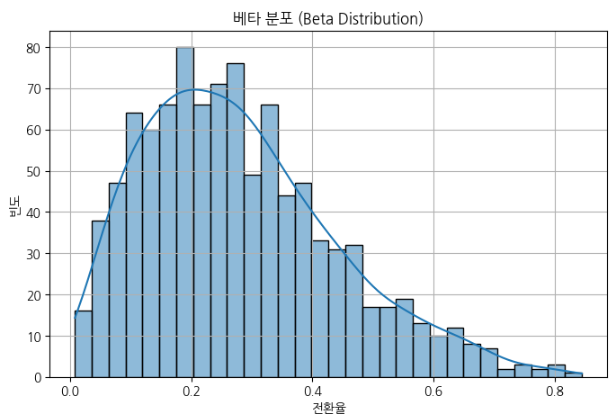
베타 분포는 0과 1 사이의 값만 가지는 연속 확률 분포.
확률적인 비율(전환율, 클릭률, 구매율 등)이나 신뢰도 분석에 자주 사용
형상 모수(α, β) 값에 따라 다양한 모양을 가질 수 있음.

→ 평균적으로 전환율이 약 28.6% 정도 될 것으로 예측.
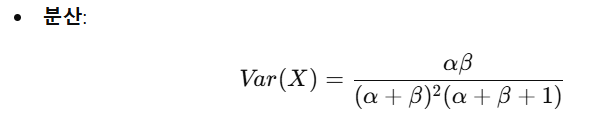
분산이 클수록 데이터가 넓게 퍼져 있고, 작을수록 데이터가 한쪽에 집중돼 있음.
마케팅 성과 예측(1)
통계적 분석 기법을 활용하여 고객 반응과 매출 성과를 예측하는 과정
→ '제안서'에 쓸 수 있음.
대표적인 분석방법
1. 회귀 분석 - 마케팅 요소(광고비, 고객참여도 등)와 성과(매출, 구매전환율 등) 간의 관계를 분석
| 종류 | 설명 | 활용예시 |
| 단순 회귀 분석 | 하나의 독립변수(X)가 종속변수(Y)에 미치는 영향을 분석하는 방법. ex) 광고비(X)와 매출(Y)의 관계를 분석. |
광고비를 100만원 증가시켰을 때 예상 매출이 얼마나 증가하는지 예측. |
| 다중 회귀 분석 | 여러 개의 독립 변수(X1, X2, X3...)가 종속 변수(Y)에 미치는 영향을 분석하는 방법. ex) 예를 들어 광고비, 방문자 수, 소셜 미디어 반응이 매출에 미치는 영향을 분석. |
광고비뿐만 아니라 SNS 활동, 이메일 마케팅이 매출 증가에 미치는 영향을 종합적으로 분석. |
2. 시계열 분석 - 일정 기간 동안의 데이터를 기반으로 미래 성과를 예측하는 방법
| 종류 | 설명 | 활용예시 |
| 이동평균법 | 과거 일정 기간 동안의 데이터를 평균 내어 미래 값을 예측하는 방식 ex) 지난 6개월간의 월별 매출 평균을 기반으로 다음 달 예상 매출을 계산. |
성수기와 비수기의 패턴을 분석하여 적절한 광고 예산을 책정. |
| ARIMA | 과거의 패턴과 추세를 분석하여 미래 값을 예측하는 대표적인 시계열 모델. ex) 매월 발생하는 매출 데이터를 학습하여 다음 달 매출을 예측. |
계절별 마케팅 전략을 수립하는데 활용. 예를 들어 연말 프로모션의 효과를 사전에 예측할 수 있음. |
3. 로지스틱 회귀 분석
- 분류문제 해결. 특히 이진 분류 문제(둘 중 하나 예측). (선형회귀 - 숫자 예측, 로지스틱회귀 - 특정범주 예측)
| 설명 | 활용예시 | |
| 로지스틱 회귀 분석 | 특정 마케팅 캠페인이 성공할 확률을 예측. (0~1사이) ex) 이메일 마케팅을 발송했을 때 고객이 제품을 구매할 확률 예측 |
이메일 제목이나 광고 문구에 따라 구매 전환율이 증가하는 패턴을 분석. |
4, 군집분석 - 유사한 고객 그룹을 묶어 마케팅 전략을 차별화
| 종류 | 설명 | 활용예시 |
| K-평균 군집화 | 고객을 비슷한 성향(소비 패턴, 관심사 등)으로 그룹화하여 타겟 마케팅을 실행하는 방식 ex) VIP 고객, 일반 고객, 신규 고객으로 나누어 맞춤형 프로모션을 적용 |
VIP 고객에게는 추가 혜택을 제공하고, 신규 고객에게는 웰컴 쿠폰을 제공. |
| 계층적 군집 분석 | 고객 데이터를 계층적으로 묶어 고객을 세분화하는 방식. ex) 온라인 쇼핑몰에서 구매 이력을 기반으로 고객을 그룹화. |
고객 세분화를 통해 맞춤형 광고 콘텐츠를 제공. |
5. 감성 분석 - 브랜드 이미지와 고객 만족도 개선
| 설명 | 활용예시 | |
| 감성 분석 | 고객 리뷰나 SNS 데이터를 분석하여 제품이나 브랜드에 대한 감정을 파악하는 기법. ex) 고객 리뷰를 분석하여 긍정/부정 감정을 판단하고, 이를 통해 제품 개선 방향을 도출. |
부정적인 피드백이 많다면 서비스 개선이 필요하며, 긍정적인 리뷰가 많은 광고 요소를 강조하여 마케팅을 강화. |
6. 생존 분석
| 설명 | 활용예시 | |
| 생존 분석 | 고객 이탈률(Churn Rate)을 분석하여 고객 유지 전략을 수립하는 기법. ex) 특정 기간 동안 고객이 서비스를 계속 사용할 확률을 예측. |
구독 기반 서비스에서 고객 이탈 위험이 높은 그룹을 식별하여 맞춤형 유지 캠페인을 실행. |
7. 의사결정나무 및 랜덤 포레스트
- 마케팅 요소가 고객 행동에 미치는 영향 분석
| 종류 | 설명 | 활용예시 |
| 의사결정나무 | 고객이 구매할 가능성이 높은 조건을 시각적으로 분석하는 방법. ex) 30대 여성 중 SNS 참여도가 높은 고객이 특정 브랜드 제품을 구매할 확률이 높은지 분석. |
고객 데이터를 기반으로 맞춤형 마케팅 캠페인을 진행 |
| 랜덤 포레스트 | 여러 개의 의사결정나무를 결합하여 더 정확한 예측을 수행하는 방법. ex) 고객의 과거 구매 기록을 바탕으로 추천 시스템을 구축. |
고객 맞춤형 상품 추천을 제공하여 매출을 증대 |
다중 회귀 분석을 활용한 마케팅 성과 예측
import pandas as pd
import numpy as np
import statsmodels.api as sm
import matplotlib.pyplot as plt
# Step 1: 데이터 생성 (광고비, 이메일 마케팅 반응률, 고객 리뷰 점수 -> 매출)
# 기업의 마케팅 성과 데이터를 활용하여 광고비, 이메일 반응률, 고객 리뷰 점수를 기반으로 매출 데이터를 생성.
data = {
"광고비": [500, 700, 800, 1000, 1200, 1500, 1800, 2000, 2300, 2500],
"이메일반응률": [3.1, 3.8, 4.2, 4.5, 5.0, 5.5, 6.0, 6.5, 7.0, 7.5],
"고객리뷰점수": [4.0, 4.2, 4.5, 4.6, 4.8, 5.0, 5.1, 5.3, 5.5, 5.7],
"매출": [50, 65, 80, 90, 110, 130, 150, 170, 190, 210]
}
df = pd.DataFrame(data)
# Step 2: 독립 변수 (X)와 종속 변수 (y) 설정
# 광고비, 이메일 마케팅 반응률, 고객 리뷰 점수를 독립 변수로 설정하고, 매출을 종속 변수로 설정.
X = df[["광고비", "이메일반응률", "고객리뷰점수"]]
y = df["매출"]
# Step 3: 상수항 추가 (회귀 모델에 필요)
# sm.add_constant(X)를 사용하여 회귀 모델에 절편(상수항)을 추가
X = sm.add_constant(X)
# Step 4: 회귀 모델 생성 및 학습
# statsmodels 라이브러리의 OLS(Ordinary Least Squares)를 활용하여 다중 회귀 분석을 수행
model = sm.OLS(y, X).fit()
# Step 5: 모델 요약 출력
# model.summary()를 출력하여 회귀 계수, R-squared 값, p-value 등을 확인
print(model.summary())
# Step 6: 예측값 생성
# 학습된 모델을 사용하여 예측된 매출 값을 데이터프레임에 추가
df["예측매출"] = model.predict(X)
# Step 7: 실제 매출 vs 예측 매출 비교 그래프
# 실제 매출과 예측 매출을 시각적으로 비교하여 모델의 성능을 평가
plt.figure(figsize=(8, 5))
plt.plot(df["매출"], label="실제 매출", marker='o')
plt.plot(df["예측매출"], label="예측 매출", linestyle='--', marker='s')
plt.xlabel("데이터 인덱스")
plt.ylabel("매출")
plt.legend()
plt.title("실제 매출 vs 예측 매출")
plt.show()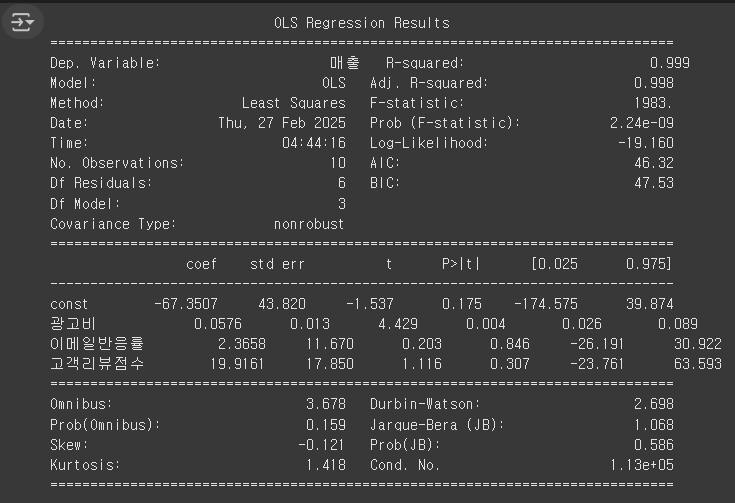
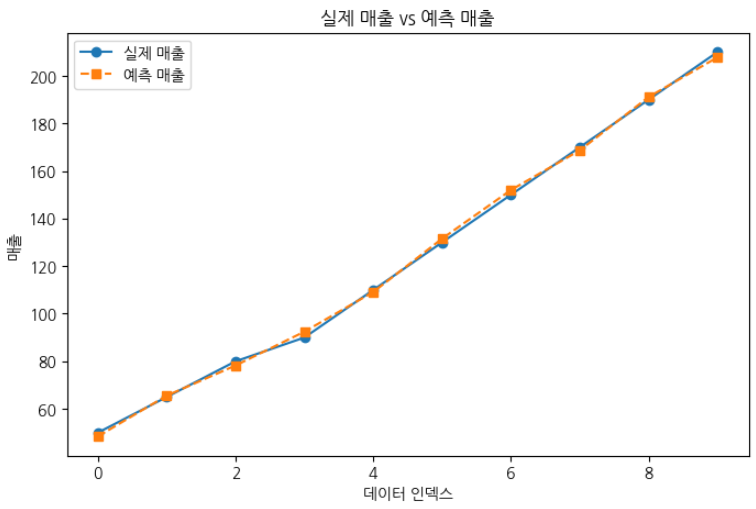
- R-squared (결정 계수): 모델의 설명력 (0~1, 1에 가까울수록 예측 성능이 좋음)
- p-value: 독립 변수들(광고비, 이메일 반응률, 고객 리뷰 점수)이 종속 변수(매출)에 유의미한 영향을 주는지 확인하는 값 (보통 0.05 미만이면 영향 있음)
- coef (회귀 계수, β 값 ): 각 독립 변수가 매출에 미치는 영향력
R-squared 값이 0.999이므로, 이 모델은 99.9%의 설명력을 가진다는 뜻.
즉, 광고비, 이메일반응률, 고객리뷰점수 3가지 변수가 매출 변동을 99.9%나 설명할 수 있음.
P-value값
광고비는 0.004이므로 유의미. 광고비는 매출에 강한 영향을 미침.
이메일 반응률은 0.846이므로 유의미하지 않음. 이메일 반응률을 매출에 큰 영향을 안 줌.
고객리뷰점수는 0.307이므로 유의미하지 않음. 고객리뷰점수도 매출에 큰 영향을 안 줌.
회귀계수 (coef값)
광고비(coef=0.0576)
광고비를 1,000원 증가시키면 매출이 약 57.6 증가한다는 뜻.
광고비는 매출에 유의미한 영향을 준다 (p-value=0.004).
이메일반응률(coef=2.3658)
이메일 반응률이 1% 증가하면 매출이 약 2.37 증가.
하지만 p-value가 너무 높아서(0.846), 실제로는 매출에 큰 영향을 주지 않을 가능성이 높음.
고객리뷰점수(coef=19.9161)
고객 리뷰 점수가 1점 올라가면 매출이 19.92 증가.
하지만 p-value가 높아서(0.307), 통계적으로 신뢰하기 어려움.
시계열 분석을 활용한 마케팅 성과 예측 (이동 평균법과 ARIMA 모델)
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import statsmodels.api as sm
from statsmodels.tsa.arima.model import ARIMA
# Step 1: 데이터 생성 (월별 매출 데이터 - 지난 36개월치)
# 기업의 지난 36개월(3년간) 월별 매출 데이터를 생성
# 매출 데이터는 점진적으로 증가하는 패턴을 가지며, 연말(12월)에 프로모션 효과로 인한 급증 현상이 반영되어 있음.
# sales는 기본적으로 200에서 시작하고, 매월 10씩 증가하는 패턴을 가짐.
# np.random.randint(-30, 30)을 추가해서 약간의 랜덤 변동성(오차)을 부여.
np.random.seed(42)
months = pd.date_range(start="2021-01", periods=36, freq="M")
sales = [200 + 10 * i + np.random.randint(-30, 30) for i in range(36)] # 기본 증가 패턴 + 랜덤 변동
sales[11] += 100 # 연말 프로모션 효과 (12월)
sales[23] += 80 # 연말 프로모션 효과 (12월)
sales[35] += 90 # 연말 프로모션 효과 (12월)
# 두 개의 리스트(months, sales)를 사용해서 데이터프레임(DataFrame)을 만든다.
# months: 날짜 정보 (2021년 1월 ~ 2023년 12월까지 36개월치)
# sales: 해당 월의 매출 데이터
# df.set_index("월", inplace=True) → "월"컬럼을 인덱스로 설정해서 시계열 분석이 쉽게 만든다.
df = pd.DataFrame({"월": months, "매출": sales})
df.set_index("월", inplace=True)
# Step 2: 이동 평균법 (Moving Average) 적용
# "이동 평균"은 일정한 기간 동안의 평균을 계속해서 계산하는 방법.
# 과거 데이터를 일정한 구간(window) 단위로 묶어서 평균을 구하는 것.
# 과거 6개월 동안의 평균 매출을 구해서 변동성을 부드럽게 만듦.
# 이 방법을 사용하면 단기적인 노이즈를 줄이고 전체적인 추세를 볼 수 있음.
# 성수기와 비수기의 변화 흐름을 쉽게 분석할 수 있다.
# 즉, 1월~6월 평균, 2월~7월 평균, 3월~8월 평균 … 이렇게 점점 이동하면서 평균을 계산.
df["이동평균_6개월"] = df["매출"].rolling(window=6).mean()
# Step 3: ARIMA 모델 학습 및 예측
# (p=2, d=1, q=2)를 사용했는데, 각각 의미는:
# p=2 → 과거 2개월의 데이터가 현재 값을 예측하는 데 영향을 줌. (AR: AutoRegressive)
# d=1 → 데이터를 1차 차분하여(변화량을 계산하여) 추세를 제거함. (I: Integrated)
# q=2 → 과거 2개월의 예측 오차를 반영. (MA: Moving Average)
model = ARIMA(df["매출"], order=(2, 1, 2)) # ARIMA(2,1,2) 모델 설정
model_fit = model.fit() # 모델 학습
forecast = model_fit.forecast(steps=3) # 향후 3개월의 매출을 예측함.
# Step 4: 시각화
# 실제 매출 (파란 선, 원형 마커)
# 6개월 이동 평균 (점선) : 노이즈를 제거하고 매출의 흐름을 부드럽게 보여줌.
# 예측 시작점 (빨간 점선) : 마지막 실제 매출 데이터 이후의 시점.
# ARIMA 예측 값 (점선, 네모 마커) : 향후 3개월 매출을 예측한 결과를 표시.
# 즉, 실제 매출과 예측 결과를 한눈에 비교할 수 있도록 시각화.
plt.figure(figsize=(10, 5))
plt.plot(df.index, df["매출"], label="실제 매출", marker="o")
plt.plot(df.index, df["이동평균_6개월"], label="이동 평균 (6개월)", linestyle="--")
plt.axvline(x=df.index[-1], color='r', linestyle="dotted", label="예측 시작점")
plt.plot(pd.date_range(start=df.index[-1], periods=4, freq="M")[1:], forecast, label="ARIMA 예측값", linestyle="dashed", marker="s")
plt.xlabel("월")
plt.ylabel("매출")
plt.legend()
plt.title("마케팅 성과 예측: 이동 평균 & ARIMA 모델")
plt.show()
# Step 5: 예측 결과 출력
# 향후 3개월의 매출 예측 값을 출력
print("향후 3개월 매출 예측 (ARIMA 모델):")
print(forecast)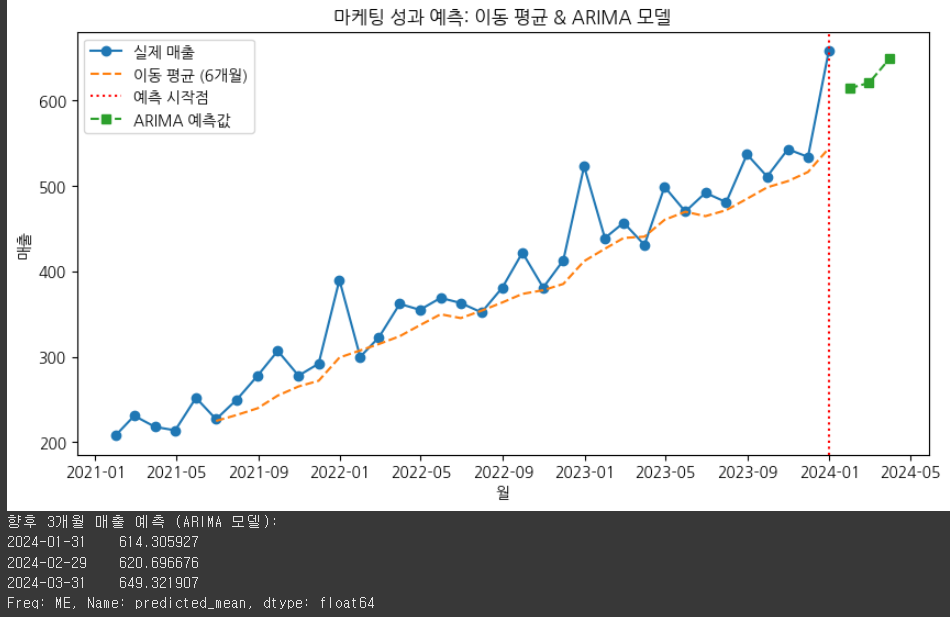
이동 평균(Moving Average) → 단기 변동을 줄이고 매출의 추세를 파악하는 데 사용됨.
ARIMA 모델 → 시계열 데이터를 기반으로 향후 3개월 매출을 예측함. (미래 값을 예측)
예측 결과 → 실제 매출 데이터와 비교하여 마케팅 전략을 세우는 데 활용 가능함.
시계열 분석 - 시간순서대로 배치되어있는 데이터. 가장 큰 특징은 인과성이 있다는 것.
이동평균 - 여러개의 데이터를 평균선을 그어버림. 들락날락 폭을 평균으로 보기 쉽게 하기 위해.
ARIMA - 좀 복잡. 최근에는 많이 안씀.
이동평균, ARIMA보다 딥러닝이 성능 갑. 회귀식은 그나마 성능 강함.
연말에는 매출이 증가한 모습이 보인다.
※ 교사학습 : 분류, 회귀 → 라벨이 있다. 종속변수가 있다.
※ 비교사학습 : 군집 (K-평균 군집화, RFM 분석, 계층적 군집분석)
로지스틱 회귀 분석을 활용한 이메일 마케팅 캠페인 성과 예측
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score, confusion_matrix, classification_report
# Step 1: 데이터 생성 (이메일 캠페인 관련 변수 -> 구매 여부 예측)
# 랜덤 데이터 생성
np.random.seed(42)
data = {
"이메일제목길이": np.random.randint(20, 80, 200), # 이메일 제목의 글자 수를 20에서 80글자 사이로 랜덤하게 200개 생성
"할인율": np.random.uniform(0, 50, 200), # 할인율(%) # 할인율을 0%에서 50%사이로 랜덤하게 200개 생성
"이메일클릭여부": np.random.choice([0, 1], size=200, p=[0.6, 0.4]), # 이메일 클릭 여부 (0: 클릭 안함, 1: 클릭) [0, 1]에서 200개 선택, 0이 나올 확률 60%, 1이 나올 확률 40%
"구매여부": np.random.choice([0, 1], size=200, p=[0.7, 0.3]) # 구매 여부 (0: 미구매, 1: 구매) 0이 70%, 1이 30% 확률로 선택됨
}
# pandas 데이터프레임(표) 생성
df = pd.DataFrame(data)
# Step 2: 독립 변수(X)와 종속 변수(y) 설정
X = df[["이메일제목길이", "할인율", "이메일클릭여부"]]
y = df["구매여부"]
# Step 3: 데이터 분할 (훈련 데이터 80%, 테스트 데이터 20%)
# train_test_split() 함수 사용하여 데이터 분할 (훈련용, 테스트용, (시험용은빠짐)) 20%가 테스트용 80%가 훈련용
# random_state=42 : 랜덤시드 고정
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# Step 4: 로지스틱 회귀 모델 생성 및 학습
model = LogisticRegression() # 로지스틱회귀모델생성
model.fit(X_train, y_train) # 훈련데이터로 로지스틱 회귀모델을 학습
# Step 5: 예측 수행
# predict(): 학습된 모델을 사용해서 테스트 데이터 X_test에 대해 예측을 수행하는 부분.
# 예측값 y_pred는 "구매 여부 (0 또는 1)"에 대한 예측값을 담고 있음.
y_pred = model.predict(X_test)
# Step 6: 모델 평가
# accuracy_score(): 모델이 얼마나 정확하게 예측했는지를 나타내는 지표. 정확도는 (정확한 예측 횟수 / 총 예측 횟수)로 계산.
# confusion_matrix(): 혼동 행렬을 구하는 함수. 모델이 예측한 값과 실제 값을 비교해 각 클래스별로 정확히 예측한 횟수와 잘못 예측한 횟수를 확인.
# classification_report(): 정밀도 (precision), 재현율 (recall), F1-score와 같은 다양한 성능 지표를 계산해서 보여주는 함수.
accuracy = accuracy_score(y_test, y_pred)
conf_matrix = confusion_matrix(y_test, y_pred)
report = classification_report(y_test, y_pred)
print(f"모델 정확도: {accuracy:.2f}")
print("\n혼동 행렬:")
print(conf_matrix)
print("\n분류 보고서:")
print(report)
# Step 7: 시각화 (혼동 행렬을 시트맵으로 시각화)
# annot=True: 각 셀에 숫자를 표시
# fmt="d": 숫자 형식을 정수로 설정
# cmap="Blues": 색상 맵을 파란색 계열로 설정
plt.figure(figsize=(5, 4))
sns.heatmap(conf_matrix, annot=True, fmt="d", cmap="Blues", xticklabels=["미구매", "구매"], yticklabels=["미구매", "구매"])
plt.xlabel("예측값")
plt.ylabel("실제값")
plt.title("로지스틱 회귀 분석 - 혼동 행렬")
plt.show()- confusion_matrix(): 혼동 행렬을 구하는 함수. 모델이 예측한 값과 실제 값을 비교해 각 클래스별로 정확히 예측한 횟수와 잘못 예측한 횟수를 확인할 수 있음.
- True Positive (TP): 실제로 구매한 사람 중 예측도 구매한 사람
- True Negative (TN): 실제로 구매하지 않은 사람 중 예측도 구매하지 않은 사람
- False Positive (FP): 실제로 구매하지 않은 사람 중 예측이 구매한 사람
- False Negative (FN): 실제로 구매한 사람 중 예측이 구매하지 않은 사람
- classification_report(): 정밀도 (precision), 재현율 (recall), F1-score와 같은 다양한 성능 지표를 계산해서 보여주는 함수.
- 정밀도(Precision): 모델이 예측한 "구매" 중 실제로 구매한 비율
- 재현율(Recall): 실제로 구매한 사람 중 모델이 정확히 예측한 비율
- F1-score: 정밀도와 재현율의 조화 평균으로, 두 지표를 균형 있게 평가하는 지표
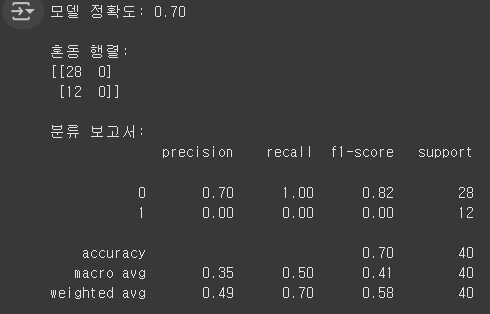
※ 혼동 행렬(Confusion Matrix) 해석:
혼동 행렬의 구조는 다음과 같다
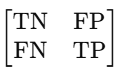
이걸 실제 값과 예측 값에 맞춰 보면
- TN (True Negative, 실제 0 → 예측도 0) = 28
→ 실제로 "미구매(0)"인 샘플 28개를 정확하게 "미구매"로 예측함. (맞춘 것) - FP (False Positive, 실제 0 → 예측 1) = 0
→ 실제로 "미구매(0)"인데 "구매(1)"로 잘못 예측한 경우 없음. (이런경우 없음) - FN (False Negative, 실제 1 → 예측 0) = 12
→ 실제로 "구매(1)"인데 "미구매(0)"로 잘못 예측한 경우 12개 있음. (틀린 것) - TP (True Positive, 실제 1 → 예측도 1) = 0
→ 실제로 "구매(1)"인 샘플을 "구매(1)"로 예측한 경우가 없음. (이런경우 없음)
※ 정확도(Accuracy) 해석:

즉, 모델이 전체 샘플 중 70%를 정확하게 예측함.
하지만 정확도가 높다고 해서 모델이 좋은 것은 아님. 이 모델은 구매(1)를 한 번도 예측하지 못함.
※ 각 지표의 의미:
| 클래스 | Precision (정밀도) | Recall (재현율) | F1-score |
| 0 (미구매) | 0.70 | 1.00 | 0.82 |
| 1 (구매) | 0.00 | 0.00 | 0.00 |
1) 정밀도
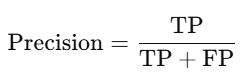
- 미구매(0) Precision = 0.70
→ 모델이 "미구매"라고 예측한 것 중 실제로 "미구매"였던 비율 (즉, 100% 정확함). - 구매(1) Precision = 0.00
→ 모델이 "구매"라고 예측한 샘플이 아예 없기 때문에 정밀도가 0.
2) 재현율
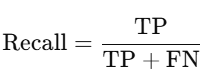
- 미구매(0) Recall = 1.00
→ 실제 "미구매"인 샘플을 100% 정확하게 맞춤. - 구매(1) Recall = 0.00
→ 실제 "구매"인 샘플 중 예측이 맞은 게 없어서 재현율이 0.
3) F1-score
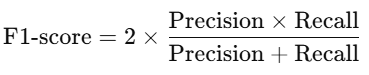
- 미구매(0) F1-score = 0.82
- 구매(1) F1-score = 0.00
F1-score는 Precision과 Recall의 조화 평균이기 때문에, 구매(1)의 F1-score가 0이라는 것은 모델이 아예 구매(1)를 예측하지 못한다는 뜻.
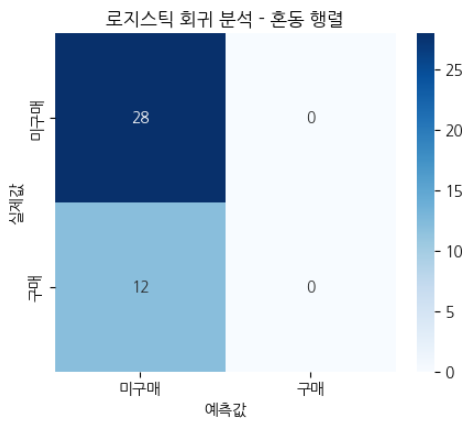
※ 혼동행렬 그래프 해석:
- 파란색이 진할수록 예측이 많이 맞았다는 의미.
- 가장 진한 파란색(TN = 28, 왼쪽 위) → 미구매(0)를 정확하게 예측한 경우가 28번.
- 옅은 파란색(FN = 12, 왼쪽 아래) → 구매(1)였는데 미구매(0)로 잘못 예측한 경우가 12번.
- 완전 흰색(FP = 0, 오른쪽 위) → 구매(1)라고 잘못 예측한 적이 없다.
- 완전 흰색(TP = 0, 오른쪽 아래) → 구매(1)를 맞춘 적이 없다.
결론적으로, 모델이 "구매(1)"를 한 번도 예측하지 못한 문제점이 있음.
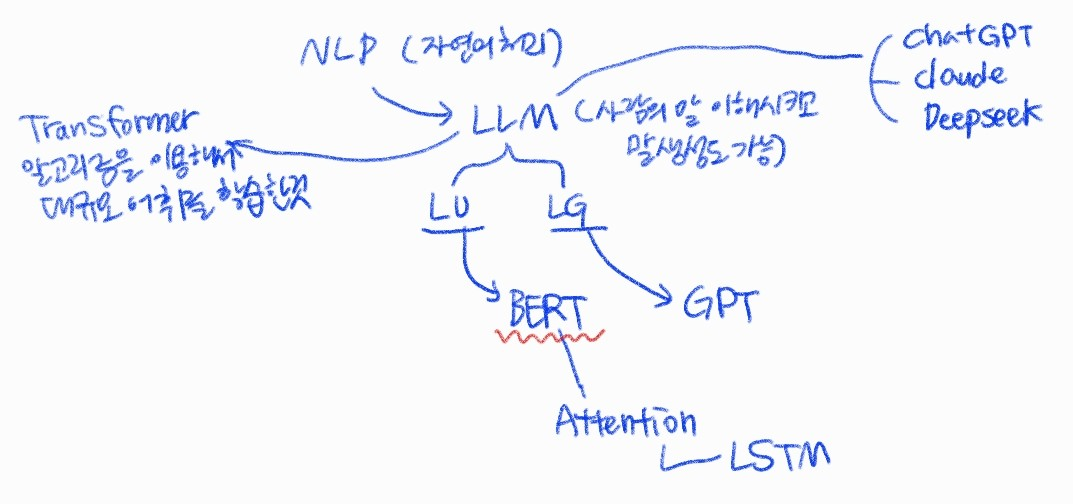
BERT 임베딩을 활용한 감성 분석을 통한 마케팅 성과 예측
import torch
from transformers import BertTokenizer, BertForSequenceClassification
from scipy.special import softmax
import pandas as pd
# Step 1: BERT 모델 및 토크나이저 로드
# nlptown/bert-base-multilingual-uncased-sentiment 모델을 사용하여 다국어 감성 분석을 수행.
# 한국어, 영어 등 여러 언어의 감정을 분석할 수 있다.
MODEL_NAME = "nlptown/bert-base-multilingual-uncased-sentiment" # 다국어 감성 분석 모델
tokenizer = BertTokenizer.from_pretrained(MODEL_NAME)
model = BertForSequenceClassification.from_pretrained(MODEL_NAME)
# Step 2: 샘플 댓글 데이터 생성
# 고객의 리뷰 및 SNS 댓글 샘플 데이터를 생성한다.
# 긍정적, 부정적, 중립적인 리뷰를 포함한다.
data = {
"댓글": [
"이 제품 정말 좋아요! 완전 만족합니다.",
"배송이 너무 느려요. 다시는 안 살 거예요.",
"가격 대비 성능이 훌륭합니다. 추천해요!",
"포장이 엉망이었어요. 기분이 나빴습니다.",
"고객 서비스가 훌륭했어요! 빠르게 해결해 줬어요."
]
}
df = pd.DataFrame(data)
# Step 3: 감성 분석 함수 정의
# BERT 토크나이저를 사용하여 입력 텍스트를 토큰화하고, 모델을 통해 감정을 예측한다.
# 모델의 출력값을 softmax 함수를 통해 감정 확률로 변환한다.
# 5단계 감정 분류(매우 부정 ~ 매우 긍정)로 분류한다.
def predict_sentiment(text):
inputs = tokenizer(text, return_tensors="pt", truncation=True, padding=True, max_length=512)
with torch.no_grad():
outputs = model(**inputs)
scores = softmax(outputs.logits.numpy())[0] # 확률값 변환
sentiment_score = scores.argmax() # 가장 높은 점수의 인덱스 선택 (0~4)
# BERT 감성 분석 모델 기준 (0: 매우 부정, 1: 부정, 2: 중립, 3: 긍정, 4: 매우 긍정)
sentiment_labels = ["매우 부정", "부정", "중립", "긍정", "매우 긍정"]
return sentiment_labels[sentiment_score], scores[sentiment_score] # 감정 라벨 및 확률값 반환
# Step 4: 댓글 감성 분석 수행
# 각 댓글을 분석하여 감정 라벨과 확률값을 반환한다.
df["감정"], df["확률"] = zip(*df["댓글"].apply(predict_sentiment))
# Step 5: 감성 분석 결과 출력
# 데이터프레임을 출력하여 댓글별 감성 분석 결과를 확인할 수 있다.
print("감정분석결과")
display(df)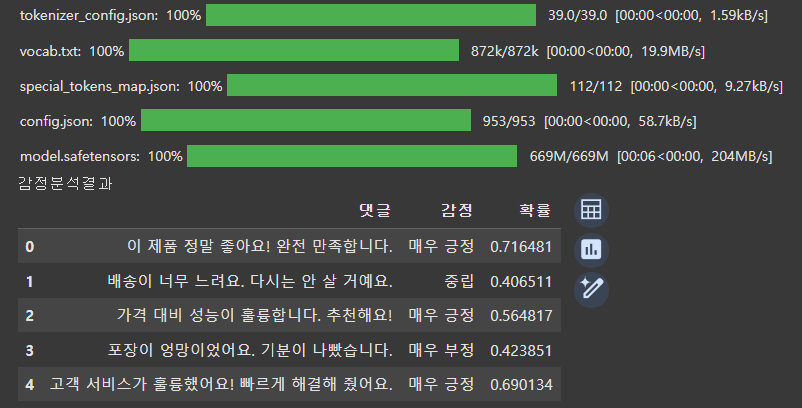
BERT 감성 분석 과정
- 토크나이징 → 문장을 숫자로 변환
- BERT 모델 예측 → 감정 점수(logits) 계산
- Softmax 변환 → 점수를 확률값(0~1)으로 변환
- 최고 확률 감정 선택 → argmax()를 사용해 최종 감정 선택
- 결과 출력 → 감정 라벨과 확률을 표로 출력
BERT 임베딩을 활용한 감성 분석 실습
- 오리발 A 감성 분석 및 파이차트 그리기
# 실습 A군 밴디스 오리발
import torch
from transformers import BertTokenizer, BertForSequenceClassification
from scipy.special import softmax
import pandas as pd
# Step 1: BERT 모델 및 토크나이저 로드
MODEL_NAME = "nlptown/bert-base-multilingual-uncased-sentiment" # 다국어 감성 분석 모델
tokenizer = BertTokenizer.from_pretrained(MODEL_NAME)
model = BertForSequenceClassification.from_pretrained(MODEL_NAME)
# Step 2: 샘플 댓글 데이터 생성
data = {
"댓글": [
"넉넉하여 잘 들어갔던 점이 좋았어요.",
"좀 쪼이기는 한데 그래야 안 벗겨질거 같네요. 잘 신을게요.",
"배송도 빠르고 좋아요. 매쉬 주머니 있어서 좋네요.",
"L사이즈 샀습니다. 발 270정도 되시는 분들이면 딱 맞을 거 같아요.",
"좋아요. 좋아요. 좋아요. 좋아요.",
"착용이 편하나 약간 무거운 편이에요. 운동 효과는 좋아요.",
"가족여행시 쓸려고 샀습니다.",
"놀러가서 바다에서 잘 쓰고 왔어요! 사용하고 물놀이 가방에 넣어서 보관하면 좋아요. 이케아 가방에 두개 들어가고도 남아요.",
"부드럽고 디자인이 좋아 아이발에 무리가 없어요.",
"신발 255를 신는데 M사이즈가 작지 않을까 걱정했는데 딱 맞네요. 실리콘 재질이라 탄성이 좋으니 조금 작게 구매해야 수영시 잘 안벗겨질거에요.",
"발사이즈 290 엑스라지 하면 됩니다.",
"작은 발에도 무난하게 잘 맞고 가벼워요.",
"빠르게 잘 받았어요. 두번째 구매도 빨리 배송 좀.",
"발 볼이 크고 실리콘이라 무거워요. 수영하고 나면 발등이 아픕니다. 급해서 산거라 배송은 빨랐어요.",
"수영수업때 사용했어요. 가성비 좋아요.",
"아직 발이 작아서 조금 크긴 하지만 보조밴드 착용해서 신으면 될것 같아요.",
"만족합니다. 고마워요. 신혼여행 때 잘 썼어요.",
"아들 수영장 준비물이에요. 정사이즈 같네요.",
"사이즈 230인데 뒤쪽이 살짝 헐렁하지만 편하고 괜찮아요. 벗겨지지 않아요.",
"깨끗하고 쓸만합니다. 저렴하고."
]
}
df = pd.DataFrame(data)
# Step 3: 감성 분석 함수 정의
def predict_sentiment(text):
inputs = tokenizer(text, return_tensors="pt", truncation=True, padding=True, max_length=512)
with torch.no_grad():
outputs = model(**inputs)
scores = softmax(outputs.logits.numpy())[0] # 확률값 변환
sentiment_score = scores.argmax() # 가장 높은 점수의 인덱스 선택 (0~4)
# BERT 감성 분석 모델 기준 (0: 매우 부정, 1: 부정, 2: 중립, 3: 긍정, 4: 매우 긍정)
sentiment_labels = ["매우 부정", "부정", "중립", "긍정", "매우 긍정"]
return sentiment_labels[sentiment_score], scores[sentiment_score] # 감정 라벨 및 확률값 반환
# Step 4: 댓글 감성 분석 수행
df["감정"], df["확률"] = zip(*df["댓글"].apply(predict_sentiment))
# Step 5: 감성 분석 결과 출력
print("밴디스오리발 감정분석결과")
display(df)
# 밴디스 오리발
import matplotlib.pyplot as plt
# 감정별 개수 집계
sentiment_counts = df["감정"].value_counts()
# 파이차트 그리기
plt.figure(figsize=(7, 7))
plt.pie(sentiment_counts, labels=sentiment_counts.index, autopct="%1.1f%%", startangle=140, colors=["red", "orange", "gray", "lightblue", "blue"])
plt.title("밴디스 오리발 감정 분석 비율")
plt.show()
# 감정별 총합 계산
sentiment_counts = df["감정"].value_counts()
# 결과 출력
print(sentiment_counts)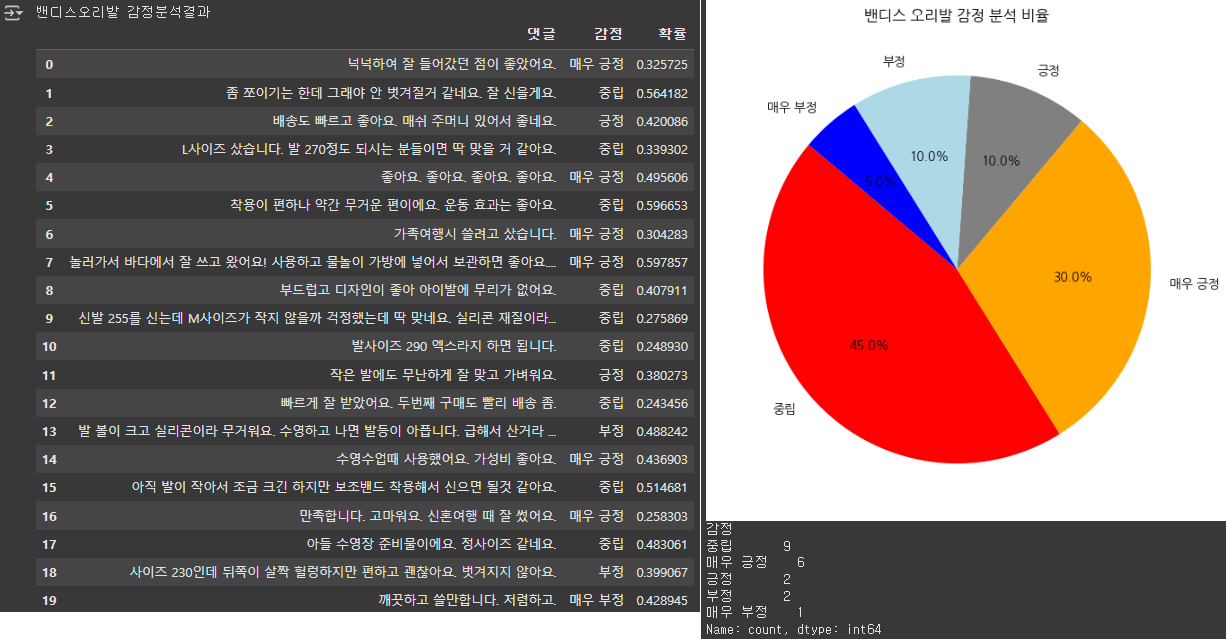
- 오리발 B 감성분석 및 파이차트 그리기
# B군 DMC 엘리트캔디 오리발
import torch
from transformers import BertTokenizer, BertForSequenceClassification
from scipy.special import softmax
import pandas as pd
# Step 1: BERT 모델 및 토크나이저 로드
MODEL_NAME = "nlptown/bert-base-multilingual-uncased-sentiment" # 다국어 감성 분석 모델
tokenizer = BertTokenizer.from_pretrained(MODEL_NAME)
model = BertForSequenceClassification.from_pretrained(MODEL_NAME)
# Step 2: 샘플 댓글 데이터 생성
data = {
"댓글": [
"디자인이 오리같이 귀여워요. 숏핏임에도 잘나가고 사이즈도 잘 맞아요.",
"잘 사용 하고 있어요. 가벼워요.",
"너무 귀여워요. 아이와 커플템입니다.",
"아주 잘쓰고 있어요. 입문용으로 추천.",
"발은 235, 운동화는 240 신는데 사이즈 딱 맞습니다.",
"우선 너무 귀여워요~~!! 사이즈가 크지않을까 싶었는데 볼이 있어서인지 잘 맞아요!",
"잘신고 수영 하고 있습니다~",
"발 볼이 넓고 발등이 넓은 편이어서 s를 주문했는데 약간 커요. 첫번 사용 때는 발등이 좀 아팠으나 두번째부터는 허벅지위주로 발차기를 하니 괜찮을 것 같습니다. 더 아프면 핀삭스를 신고 착용하려고 했어요.",
"짧아서 간편히 들고 다닐 수 있고 가벼워서 좋아요. 발목에도 무리 없고요. 평소 240 신는데 딱 맞아요. 그랴도 물에서는 괜찮아요~",
"발등이 높아서 살짝 아픈듯 하지만 수영할 때 불편함은 없고 슉슉 잘 나갑니다!",
"처음에는 딱 맞아서 좋았는데 시간지나니 좀 늘어나는거같기도 해요. 강습받을때 매우 잘 쓰고 있습니다.",
"잘 맞고 잘 나가서 만족합니다.",
"패디 좋아하시는 분은 발톱이 아파요.",
"수영 강습 때 사용하려고 샀는데 발목 아픔도 심하지 않고 무엇보다 귀여워서 좋습니다! 내 오리발이 제일 귀엽다!!!!",
"35-40 신는데 xs 주문했습니다. 밖에선 딱 낀 느낌인데 물속에선 괜찮아요.",
"어머니가 수영배우셔서 선물로 사드렸어요. 처음 사용할 때는 발이 아프셨다고 했는데, 두번째 사용부터는 편하다고 하셨어요.",
"배송이 왔는데 다른 송장이 붙어있는 채로 그 위에 제 송장을 붙여서 왔어요. 안에 있는 상자도 다 찌그러져서 왔구요. 속이 상한데 배송 중 상자가 찌그러져서 다시 포장한 걸까요?",
"살짝 큰가봐요. 발등이 쓸려요. 근데 진짜 이쁘고 슉슉 잘 나감.",
"마음에 들어요. 근데 숏핀 가방이 망사였음 하는 바램입니다.",
"수영수업시간에 사용하려고 구매했어요. 처음엔 약간 작았는데 사용하니 조금 늘어나요."
]
}
df = pd.DataFrame(data)
# Step 3: 감성 분석 함수 정의
def predict_sentiment(text):
inputs = tokenizer(text, return_tensors="pt", truncation=True, padding=True, max_length=512)
with torch.no_grad():
outputs = model(**inputs)
scores = softmax(outputs.logits.numpy())[0] # 확률값 변환
sentiment_score = scores.argmax() # 가장 높은 점수의 인덱스 선택 (0~4)
# BERT 감성 분석 모델 기준 (0: 매우 부정, 1: 부정, 2: 중립, 3: 긍정, 4: 매우 긍정)
sentiment_labels = ["매우 부정", "부정", "중립", "긍정", "매우 긍정"]
return sentiment_labels[sentiment_score], scores[sentiment_score] # 감정 라벨 및 확률값 반환
# Step 4: 댓글 감성 분석 수행
df["감정"], df["확률"] = zip(*df["댓글"].apply(predict_sentiment))
# Step 5: 감성 분석 결과 출력
print("DMC 엘리트캔디 오리발 감정분석결과")
display(df)
# 파이차트 그리기
sentiment_counts = df["감정"].value_counts()
plt.figure(figsize=(7, 7))
plt.pie(sentiment_counts, labels=sentiment_counts.index, autopct="%1.1f%%",
startangle=140, colors=["red", "orange", "gray", "lightblue", "blue"])
plt.title("DMC 엘리트캔디 오리발 감정 분석 비율")
plt.show()
# 감정별 총합 계산
sentiment_counts = df["감정"].value_counts()
# 결과 출력
print(sentiment_counts)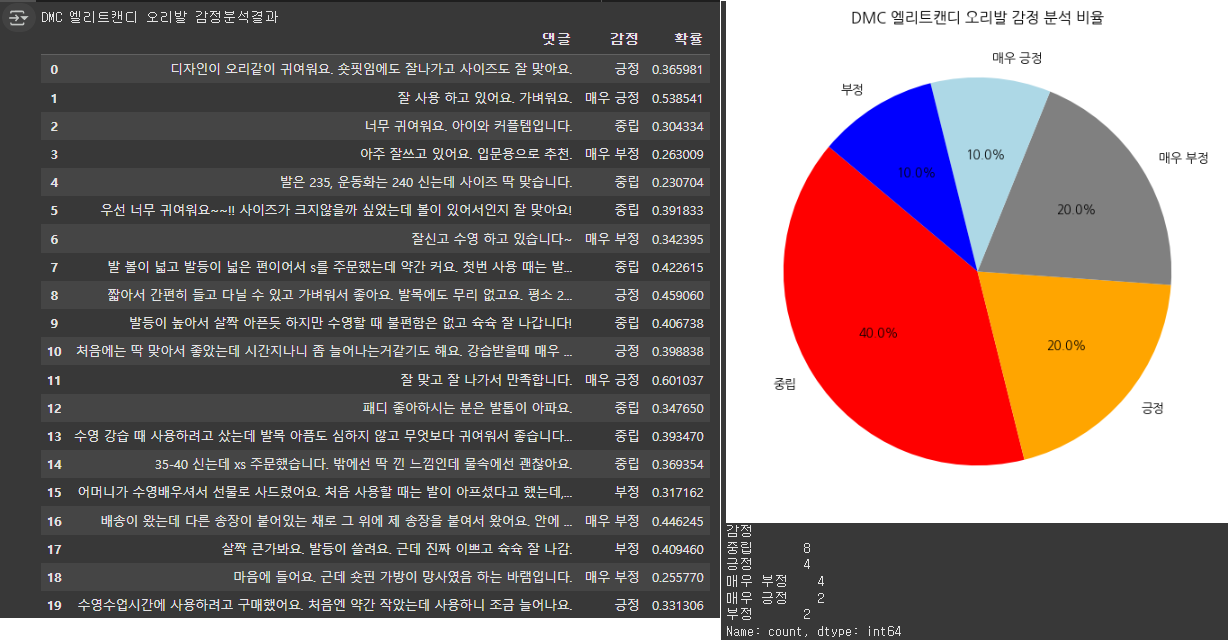
- 오리발 A,B 감정 분석 결과 비교
import numpy as np
import matplotlib.pyplot as plt
# 두 개의 감정 분석 결과
sentiment_counts_A = {"매우 부정": 1, "부정": 2, "중립": 9, "긍정": 2, "매우 긍정": 6} #밴디스오리발 데이터셋 결과
sentiment_counts_B = {"매우 부정": 4, "부정": 2, "중립": 8, "긍정": 4, "매우 긍정": 2} # DMC 엘리트캔디 오리발 데이터셋 결과
# 감정 라벨
labels = ["매우 부정", "부정", "중립", "긍정", "매우 긍정"]
# 각 감정에 대한 빈도수 리스트 만들기
values_A = [sentiment_counts_A[label] for label in labels]
values_B = [sentiment_counts_B[label] for label in labels]
# 막대그래프 그리기
x = np.arange(len(labels)) # X축 인덱스
width = 0.35 # 막대 너비
fig, ax = plt.subplots(figsize=(8, 5))
bars1 = ax.bar(x - width/2, values_A, width, label="밴디스 오리발", color="blue", alpha=0.7)
bars2 = ax.bar(x + width/2, values_B, width, label="DMC 엘리트캔디 오리발", color="orange", alpha=0.7)
# 그래프 세부 설정
ax.set_xlabel("감정")
ax.set_ylabel("댓글 수")
ax.set_title("감정 분석 비교 (A vs B)")
ax.set_xticks(x)
ax.set_xticklabels(labels)
ax.legend()
# 그래프 출력
plt.show()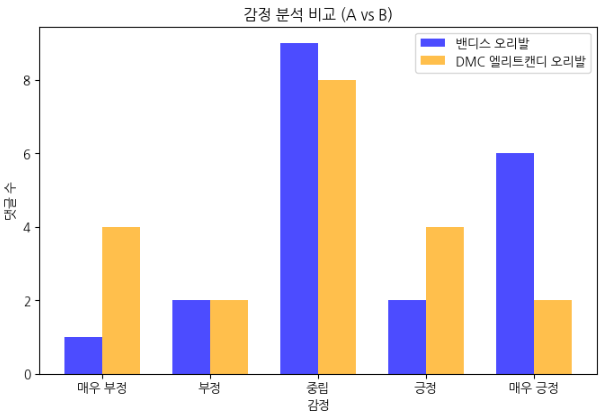
< 감성 분석 목적 >
본 분석은 밴디스 오리발과 DMC 엘리트캔디 오리발의 리뷰를 BERT 임베딩을 활용하여 감성분석을 함으로써 두 제품간의 고객 반응을 비교하고자 하였다.
밴디스 오리발은 숏핀 오리발 중 가장 저렴한 제품이다. (네이버 스토어 가격 19,800원)
DMC 엘리트캔디 오리발은 DMC 브랜드 제품중에서도 중상위 등급의 제품이다. (네이버 스토어 가격 88,000원)
< 두 제품의 비교 의견 >
# 밴디스 오리발과 DMC 엘리트캔디 오리발 둘 다 중립적인 반응이 가장 많다.
# DMC 엘리트캔디 오리발은 긍정적인 반응과 부정적인 반응이 갈리는 모습을 보인다. 즉, 호불호가 강한 모습을 보여준다.
# 밴디스 오리발은 매우 긍정 평가가 긍정보다 많다. 즉, 만족하는 사람들은 아주 만족하는 경향이 있다.
# 밴디스 오리발은 DMC 엘리트캔디 오리발보다 부정적인 반응이 적은 것을 확인할 수 있다.
< 결론 >
결과적으로 저렴한 밴디스 오리발이 DMC 앨리트캔디 오리발보다 고객 반응이 더 좋았으며, 더 합리적인 선택이라는 결론을 감성분석 비교를 통해 확인할 수 있었다.
하지만 BERT 모델의 데이터 감성분석에서 일부 오류가 나타났다.
예를 들어 밴디스 오리발의 경우 ‘깨끗하고 쓸만합니다. 저렴하고’ 라는 문구를 ‘매우 부정’으로 인식하였다.
DMC 엘리트 캔디 오리발의 경우에도 ‘아주 잘 쓰고 있어요. 입문용으로 추천.’ 이라는 문구를 ‘매우 부정’으로 인식하였다.
또한 네이버 별점은 5점인데 실제 감성분석에서는 중립으로 나타나는 경우가 많아 별점과 리뷰감성분석 결과의 차이가 나타나는 것이 확인되었다.
'데이터 분석 part' 카테고리의 다른 글
| * 태블로 실습 / Chart.js를 이용한 웹페이지 실습 (0) | 2025.03.06 |
|---|---|
| Tableau 기본 사용법 (1) | 2025.03.05 |
| 마케팅 데이터의 주요 지표 분석 (보고서 실습) (2) | 2025.02.27 |
| 상관관계의 이해, 상관분석 / 웹시스템 이용한 마케팅 데이터 획득 이해 (0) | 2025.02.25 |
| 회귀분석 (단순회귀분석과 다중회귀분석) (1) | 2025.02.25 |